
【题目】选择适当的方法解下列方程:
(1)![]() ;(2)
;(2)![]()
(3)![]() ;(4)
;(4)![]() .
.
【答案】(1)![]() =
=![]() ,
,![]() =
=![]() ;(2)
;(2)![]() =1,
=1,![]() =-9;(3)
=-9;(3)![]() =
=![]() ,
,![]() =
=![]() ;(4)
;(4)![]() =1,
=1,![]() =
=![]() .
.
【解析】
(1)根据直接开平方法可以解答此方程;
(2)因式分解法求解可得;
(3)根据公式法可以解答此方程;
(4)因式分解法求解可得.
(1)7(2x3)2=28,
(2x3)2=4,
∴2x3=±2,
解得:![]() =
=![]() ,
,![]() =
=![]() ;
;
(2)![]()
(x1)(x+9)=0,
∴x1=0或x+9=0,
解得:x=1或x=9;
(3)2x2+1=2![]() ,
,
2x22![]() +1=0,
+1=0,
∵a=2,b=2![]() ,c=1,
,c=1,
∴△=(2![]() )24×2×1=12>0,
)24×2×1=12>0,
∴x=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() ;
;
(4)![]() ,
,
(x1)2=2x(x1),
∴(x1)2+2x(x1)=0,
∴(x1)(x1+2x)=0,即(x1)(3x1)=0,
则x1=0或3x1=0,
解得:x=1或x=![]() .
.


科目:初中数学 来源: 题型:
【题目】为了加强建设“经济强、环境美、后劲足、群众富”的实力城镇,聚力脱贫攻坚,全面完成脱贫任务,某乡镇特制定一系列帮扶计划。现决定将A、B两种类型鱼苗共320箱运到某村养殖,其中A种鱼苗比B种鱼苗多80箱。
(1)求A种鱼苗和B种鱼苗各多少箱?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批鱼苗全部运往同一目的地。已知甲种货车最多可装A种鱼苗40箱和B种鱼苗10箱,乙种货车最多可装A种鱼苗和B种鱼苗各20箱。如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元,则安排甲、乙两种货车有哪几种不同的方案?并说明选择哪种方案可使运输费最少?最少运输费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】★若两个扇形满足弧长的比等于它们半径的比,则称这两个扇形相似.如图,如果扇形AOB与扇形A1O1B1是相似扇形,且半径OA∶O1A1=k(k为不等于0的常数).那么下面四个结论:①∠AOB=∠A1O1B1;②△AOB∽△A1O1B1;③![]() =k;④扇形AOB与扇形A1O1B1的面积之比为k2.成立的个数为( )
=k;④扇形AOB与扇形A1O1B1的面积之比为k2.成立的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
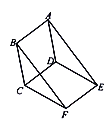
【题目】如图,已知平行四边形ABCD与平行四边形DCFE的周长相等,且![]() BAD=60°,
BAD=60°,![]() CFE=110°,则下列结论:①四边形ABFE为平行四边形;②
CFE=110°,则下列结论:①四边形ABFE为平行四边形;②![]() ADE是等腰三角形;③平行四边形ABCD与平行四边形DCFE全等;④
ADE是等腰三角形;③平行四边形ABCD与平行四边形DCFE全等;④![]() DAE=25°.其中正确的结论是.__________(填正确结论的序号)
DAE=25°.其中正确的结论是.__________(填正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
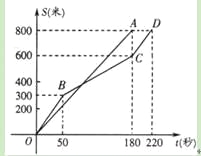
A. 小莹的速度随时间的增大而增大B. 小梅的平均速度比小莹的平均速度大
C. 在起跑后180秒时,两人相遇D. 在起跑后50秒时,小梅在小莹的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
(1)求证:AE=BE;
(2)求证:FE是⊙O的切线;
(3)若FE=4,FC=2,求⊙O的半径及CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.

A. 96 B. 204 C. 196 D. 304
查看答案和解析>>
科目:初中数学 来源: 题型:
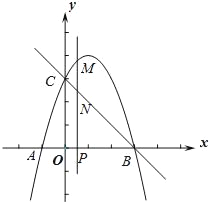
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式和直线BC的解析式;
(2)当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直角三角形时,求m的值;
(3)当以C、O、M、N为顶点的四边形是以OC为一边的平行四边形时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com