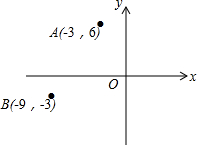Question

2．如图，在平面直角坐标系中，已知点A（-3，6），B（-9，-3），以原点O为位似中心，相似比为$\frac{1}{3}$，把△ABO缩小，则点A的对应点A′的坐标是（　　）

• A． （-1，2）
• B． （-1，2）或（1，-2）
• C． （-9，18）
• D． （-9，18）或（9，-18）

Answer 1

分析 根据在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k解答．

解答 解：∵点A的坐标为（-3，6），以原点O为位似中心，相似比为$\frac{1}{3}$，把△ABO缩小，
∴点A的对应点A′的坐标为（-3×$\frac{1}{2}$，6×$\frac{1}{2}$）或（-3×（-$\frac{1}{2}$），6×（-$\frac{1}{2}$）），
即（-1，2）或（1，-2），
故选：B．

点评 本题考查的是位似变换的性质，掌握在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k是解题的关键．