
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
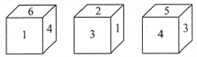
【题目】有一个正方体的六个面上分别标有数字 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字
,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字 ![]() 的面所对面上的数字记为
的面所对面上的数字记为 ![]() ,
, ![]() 的面所对面上数字记为
的面所对面上数字记为 ![]() ,那么
,那么 ![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,已知△ABC中,AC=BC=13,AB=10,△ABC的顶点A、B分别在射线OM、ON上,当点B在ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
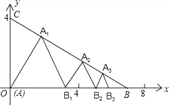
【题目】如图,已知,点A(0,0)、B(4![]() ,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
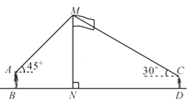
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7 m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5 m,看旗杆顶部M的仰角为30°.两人相距30米且位于旗杆两侧(点B,N,D在同一条直线上).求旗杆MN的高度.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果保留整数)
≈1.732,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一三角形纸片ABC,∠A=70°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两个纸片均为等腰三角形,则∠C的度数可以是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图所示,直线y1=-2x+3和直线y2=mx-1分别交y轴于点A,B,两直线交于点C(1,n).
(1)求m,n的值;
(2)求ΔABC的面积;
(3)请根据图象直接写出:当y1<y2时,自变量的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示
(1)家与图书馆之间的路程为多少m,小玲步行的速度为多少m/min;
(2)求小东离家的路程y关于x的函数解析式,并写出自变量的取值范围;
(3)求两人相遇的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com