
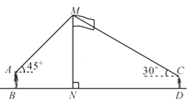
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7 m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5 m,看旗杆顶部M的仰角为30°.两人相距30米且位于旗杆两侧(点B,N,D在同一条直线上).求旗杆MN的高度.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果保留整数)
≈1.732,结果保留整数)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】课堂上李老师给出了一道整式求值的题目,李老师把要求的整式(7a3-6a3b+3a2b)-(-3a3-6a3b+3a2b+10a3-3)写完后,让王泓同学顺便给出一组![]() 的值,老师自己说答案,当王泓说完:“
的值,老师自己说答案,当王泓说完:“![]() ”后,李老师不假思索,立刻就说出答案:“3”。同学们觉得不可思议,李老师用坚定的口吻说:“这个答案准确无误。”聪明的同学们,你能说出其中的道理吗?
”后,李老师不假思索,立刻就说出答案:“3”。同学们觉得不可思议,李老师用坚定的口吻说:“这个答案准确无误。”聪明的同学们,你能说出其中的道理吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种汽车可装油400L,若汽车每小时的用油量为x(L).(1)用油量y(h)与每小时的用油量x(L)的函数关系式为______________;(2)若每小时的用油量为20L,则这些油可用的时间为______________;(3)若要使汽车继续行驶40h不需供油,则每小时用油量的范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蓄电池的电压为定植,使用此电源时,电流I(A)和电阻R(![]() )成反比例函数关系,且当I=4A,R=5
)成反比例函数关系,且当I=4A,R=5![]() .
.
(1)蓄电池的电压是多少?请你写出这一函数的表达式.
(2)当电流喂A时,电阻是多少?
(3)当电阻是10![]() .时,电流是多少?
.时,电流是多少?
(4)如果以此蓄电池为电源的用电器限制电流不超过10A,那么用电器的可变电阻应该控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元/件。试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售数量就减少10件。
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(1)k的值为______ ;
(2)判断点B(-1,6)是否在这个函数的图象上,并说明理由;
(3)当x<3时,直接写出y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,横坐标与纵坐标都是整数的点![]() 称为整点,如果将二次函数
称为整点,如果将二次函数![]() 的图象与x轴所围成的封闭图形染成红色,则此红色区域内部及其边界上的整点个数有______ 个
的图象与x轴所围成的封闭图形染成红色,则此红色区域内部及其边界上的整点个数有______ 个![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 和
和![]() 两点.
两点.
观察图象可知:①当![]() 或
或![]() 时,
时,![]() ;②当
;②当![]() 或
或![]() 时,
时,![]() ,即通过观察函数的图象,可以得到不等式
,即通过观察函数的图象,可以得到不等式![]() 的解集.
的解集.
有这样一个问题:求不等式![]() 的解集.
的解集.
某同学根据学习以上知识的经验,对求不等式![]() 的解集进行了探究.
的解集进行了探究.
下面是他的探究过程,请将(![]() )、(
)、(![]() )、(
)、(![]() )补充完整:
)补充完整:
(![]() )将不等式按条件进行转化:
)将不等式按条件进行转化:
当![]() 时,原不等式不成立.
时,原不等式不成立.
当![]() 时,原不等式可以转化为
时,原不等式可以转化为![]() .
.
当![]() 时,原不等式可以转化为
时,原不等式可以转化为![]() .
.
(![]() )构造函数,画出图象.
)构造函数,画出图象.
设![]() ,
,![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
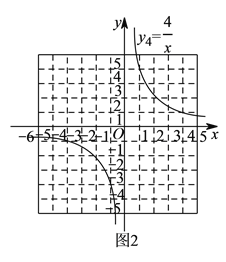
双曲线![]() 如图
如图![]() 所示,请在此坐标系中画出抛物线
所示,请在此坐标系中画出抛物线![]() .(不用列表)
.(不用列表)
(![]() )确定两个函数图象公共点的横坐标.
)确定两个函数图象公共点的横坐标.
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足![]() 的所有
的所有![]() 的值为__________.
的值为__________.
(![]() )借助图象,写出解集.
)借助图象,写出解集.
结合(![]() )的讨论结果,观察两个函数的图象可知:不等式
)的讨论结果,观察两个函数的图象可知:不等式![]() 的解集为__________.
的解集为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com