
【题目】观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.

科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题
已知:如图1,![]() ,
,![]() .求证:
.求证:![]() .
.

老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线![]() ,然后在平行线间画了一点
,然后在平行线间画了一点![]() ,连接
,连接![]() 后,用鼠标拖动点
后,用鼠标拖动点![]() ,分别得到了图2,3,4,小颖发现图3正是上面题目的原型,于是她由上题的结论猜想到图2和4中的
,分别得到了图2,3,4,小颖发现图3正是上面题目的原型,于是她由上题的结论猜想到图2和4中的![]() 、
、![]() 与
与![]() 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小颖操作探究的基础上,继续完成下面的问题:
①猜想图2中![]() 、
、![]() 与
与![]() 之间的数量关系并加以证明;
之间的数量关系并加以证明;
②补全图4,直接写出![]() 、
、![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在四边形ABFC中,![]() =90
=90![]() 的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE

(1)试探究,四边形BECF是什么特殊的四边形;
(2)当![]() 的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
(特别提醒:表示角最好用数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米.假设她们的眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)( )
≈1.732)( )
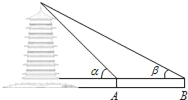
A. 36.21米 B. 37.71米 C. 40.98米 D. 42.48米
查看答案和解析>>
科目:初中数学 来源: 题型:
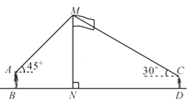
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7 m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5 m,看旗杆顶部M的仰角为30°.两人相距30米且位于旗杆两侧(点B,N,D在同一条直线上).求旗杆MN的高度.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果保留整数)
≈1.732,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,![]() 轴于点C,交的图象于点
轴于点C,交的图象于点![]() 轴于点D,交的图象于点B,当点P在的图象上运动时,下列结论错误的是( )
轴于点D,交的图象于点B,当点P在的图象上运动时,下列结论错误的是( )

A. ![]() 与
与![]() 的面积相等
的面积相等
B. 当点A是PC的中点时,点B一定是PD的中点
C. 只有当四边形OCPD为正方形时,四边形PAOB的面积最大
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了提高绿化品位,美化环境,准备将一块周长为114 m的长方形草地,设计成长和宽分别相等的9块长方形(如图所示),种上各种花卉,经市场预测,每平方米绿化费为100元.
(1)求出每个小长方形的长和宽;
(2)请计算出完成这块草地的绿化工程预计投入资金多少元.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块长为a(cm),宽为b(cm)(a>b)的矩形黑板的四周,镶上宽为x(cm)的木板,得到一个新的矩形.
(1)试用含a,b,x的代数式表示新矩形的长和宽;
(2)试判断原矩形的长、宽与新矩形的长、宽是不是比例线段,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com