搜索
【题目】如图，在△ABC中，AC＝BC，AB⊥x轴，垂足为A.反比例函数y＝
(x＞0)的图象经过点C，交AB于点D.已知AB＝4，BC＝
.
(1)若OA＝4，求k的值；
(2)连接OC，若BD＝BC，求OC的长．
参考答案：
【答案】(1)k＝5(2) 
【解析】试题分析:本题主要考查反比例函数图象和性质,(1)根据等腰三角形的性质求出点C的纵坐标,再由OA=4得出点C的坐标代入解析式即可求解,(2)先设出A点坐标,再根据BC=BD表示出点D的坐标,由勾股定理可知CE=
从而表示出C点坐标,把点C和点D坐标代入解析式求出m的值,根据点C的坐标求OC.
(1)如图，作CE⊥AB，垂足为E.作CF⊥x轴，垂足为F.∵AC＝BC，AB＝4，∴AE＝BE＝2.在Rt△BCE中，BC＝
，BE＝2，由勾股定理得CE＝
.∵OA＝4，∴OF＝OA－CE＝，∴C点的坐标为
.∵点C在y＝
的图象上，∴k＝5.
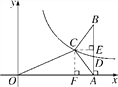
(2)设A点的坐标为(m，0)．∵BD＝BC＝，∴AD＝，∴D，C两点的坐标分别为
，
.∵点C，D都在y＝的图象上，∴m＝2
，解得m＝6，∴C点的坐标为
，∴OF＝
，CF＝2.在Rt△OFC中，OC2＝OF2＋CF2，∴OC＝
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某数学课外活动小组在做气体压强实验时，获得压强p(Pa)与体积V(cm3)之间有下列对应数据：
p(Pa)
…
1
2
3
4
5
…
V(cm3)
…
6
3
2
1.5
1.2
…
根据表中提供的信息，回答下列问题：
(1)猜想p与V之间的关系，并求出函数关系式；
(2)当气体的体积是12cm3时，压强是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y＝－x＋b与反比例函数y＝
(x＞0)的图象交于A，B两点，与x轴、y轴分别交于C，D两点，连接OA，OB，过A作AE⊥x轴于点E，交OB于点F，设点A的横坐标为m.(1)b＝________(用含m的代数式表示)；
(2)若S△OAF＋S四边形EFBC＝4，则m的值是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】加、减、乘、除是我们常用的四种运算，它们分别用＋、－、×、÷来表示．现在我们来规定一种新的运算※，规定：a※b＝a2－ab，如果1※x＝1，求x的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】点P（a，2）和点Q（4，b）关于x轴对称，则a+b=________
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y＝kx＋b的图象与反比例函数y＝
的图象在第一象限交于点A(4，2)，与y轴的负半轴交于点B，且OB＝6.(1)求函数y＝
和y＝kx＋b的解析式；(2)已知直线AB与x轴相交于点C，在第一象限内，求反比例函数y＝
的图象上一点P，使得S△POC＝9.
-
科目： 来源： 题型：
查看答案和解析>>【题目】当x=2时，ax+3的值是5，当x= -2时，代数式ax-3的值是( )
A. -5B. -1C. 1D. 2
相关试题
