
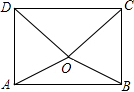
 如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长2$\sqrt{7}$d.
如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长2$\sqrt{7}$d. 分析 由等腰三角形的性质求出∠OBC=∠OCB,由矩形的性质求出AD=BC,∠ABC=∠DCB=90°,求出∠ABO=∠DCO,根据SAS推出△ABO≌△DCO,得出OA=OB,过O作MN⊥AB与N交CD于M,则AN=BN,NM⊥CD,OM=3d,ON=d,由勾股定理求出BN,得出AB,再由勾股定理求出AC即可.
解答 证明:∵OD=OC,
∴O在CD的垂直平分线线上,∠ODC=∠OCD,
∵四边形ABCD是矩形,
∴AD=BC,∠ABC=∠ADC=∠BCD=90°,
∴∠ADC-∠ODC=∠BCD-∠OCD,
即∠ADO=∠BCO,
在△ADO和△BCO中,
$\left\{\begin{array}{l}{AD=BC}&{\;}\\{∠ADO=∠BCO}&{\;}\\{OD=OC}&{\;}\end{array}\right.$,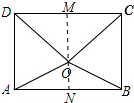
∴△ADO≌△BCO(SAS),
∴OA=OB,
∴O在AB的垂直平分线上,
过O作MN⊥AB与N交CD于M,如图所示:
则AN=BN,NM⊥CD,OM=3d,ON=d,
∴BC=MN=3d+d=4d,BN=$\sqrt{O{B}^{2}-O{N}^{2}}$=$\sqrt{(2d)^{2}-{d}^{2}}$=$\sqrt{3}$d,
∴AB=AN+BN=2$\sqrt{3}$d,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{(2\sqrt{3}d)^{2}+(4d)^{2}}$=2$\sqrt{7}$d;
故答案为:2$\sqrt{7}$d.
点评 本题考查了矩形的性质,全等三角形的性质和判定的应用,勾股定理;解此题的关键是推出△ABO≌△DCO,由勾股定理求出BN得出AB.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:选择题
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:判断题
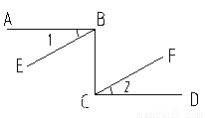
如图,从下列条件中:(1)AB∥CD, (2)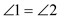 ,(3)BE∥CF任选两个作为条件,另一个作为结论,编一道数学题,并说明理由。
,(3)BE∥CF任选两个作为条件,另一个作为结论,编一道数学题,并说明理由。
已知:
结论:
理由:
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,已知AB∥CD,则∠A、∠E、∠D之间的数量关系为( )
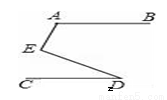
A. ∠A+∠E+∠D=360° B. ∠A+∠E+∠D=180° C. ∠A+∠E﹣∠D=180° D. ∠A﹣∠E﹣∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
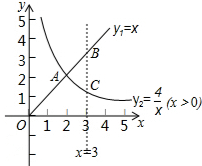 如图所示,函数y1=x(x>0),y2=$\frac{4}{x}$(x>0)的图象交于点A,与直线x=3分别交于B,C两点,给出以下四个结论:
如图所示,函数y1=x(x>0),y2=$\frac{4}{x}$(x>0)的图象交于点A,与直线x=3分别交于B,C两点,给出以下四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com