
 如图是一个正方体的展开图,标注了字母“a”的面是正方体的正面,已知正方体相对两个面上的代数式的值相等.求a+$\sqrt{x+y}$的值.
如图是一个正方体的展开图,标注了字母“a”的面是正方体的正面,已知正方体相对两个面上的代数式的值相等.求a+$\sqrt{x+y}$的值. 分析 正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答列方程组求出x、y的值,再确定出a的值,然后代入代数式进行计算即可得解.
解答 解:由题意得,$\left\{\begin{array}{l}{y=2x-5①}\\{5-x=y+1②}\end{array}\right.$,
①代入②得,5-x=2x-5+1,
解得x=3,
将x=3代入①得,y=2×3-5=1,
所以,$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,
又∵正方体相对两个面上的代数式的值相等,
∴a=3,
所以,a+$\sqrt{x+y}$=3+$\sqrt{3+1}$=3+2=5.
点评 本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.


科目:初中数学 来源: 题型:选择题
 如图,在x轴上有两点A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△AEC和等腰△BFC,顶点E,F恰好落在反比例函数y=-$\frac{5}{x}$(x<0)和y=$\frac{2}{x}$(x>0)的图象上,连结EF,在整个运动过程中,线段EF长度的变化情况是( )
如图,在x轴上有两点A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△AEC和等腰△BFC,顶点E,F恰好落在反比例函数y=-$\frac{5}{x}$(x<0)和y=$\frac{2}{x}$(x>0)的图象上,连结EF,在整个运动过程中,线段EF长度的变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
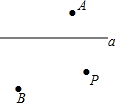 如图,平面上有直线a及直线a外的三点A、B、P.
如图,平面上有直线a及直线a外的三点A、B、P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 | |
| 男生 | 2 | 8 | 7 | 95% | 40% | |
| 女生 | 7.92 | 1.99 | 8 | 96% | 36% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数;用max{a,b,c}表示这三个数中最大的数.
对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数;用max{a,b,c}表示这三个数中最大的数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在20km的越野比赛中,甲乙两选手均跑完全程,他们的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,解答下列问题:
在20km的越野比赛中,甲乙两选手均跑完全程,他们的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com