
 如图,在x轴上有两点A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△AEC和等腰△BFC,顶点E,F恰好落在反比例函数y=-$\frac{5}{x}$(x<0)和y=$\frac{2}{x}$(x>0)的图象上,连结EF,在整个运动过程中,线段EF长度的变化情况是( )
如图,在x轴上有两点A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△AEC和等腰△BFC,顶点E,F恰好落在反比例函数y=-$\frac{5}{x}$(x<0)和y=$\frac{2}{x}$(x>0)的图象上,连结EF,在整个运动过程中,线段EF长度的变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
分析 先过点E作EG⊥AO于G,过点F作FH⊥BC于H,再设E(x,-$\frac{5}{x}$),得出F(x+3,$\frac{2}{x+3}$),分三种情况讨论:当-3<x<-$\frac{5}{3}$时,当x=-$\frac{5}{3}$时,当-$\frac{5}{3}$<x<3时,分别判断线段EF长度的变化情况.
解答 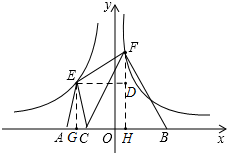 解:过点E作EG⊥AO于G,过点F作FH⊥BC于H,则CG=$\frac{1}{2}$AC,CH=$\frac{1}{2}$BC,
解:过点E作EG⊥AO于G,过点F作FH⊥BC于H,则CG=$\frac{1}{2}$AC,CH=$\frac{1}{2}$BC,
又∵A(-3,0)和B(3,0),
∴GH=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3,
当EF∥AB时,四边形EFHG是矩形,
此时,EF=GH=3,
设E(x,-$\frac{5}{x}$),则F(x+3,$\frac{2}{x+3}$),
∴在反比例函数y=-$\frac{5}{x}$中,当y=3时,x=-$\frac{5}{3}$;
当-3<x<-$\frac{5}{3}$时,过点E作ED⊥FH于D,
动点C在线段AB上从点A向点B运动时,DF的长减小,故Rt△DEF中,EF的长减小;
当x=-$\frac{5}{3}$时,EF的长最小,最小值为3;
当-$\frac{5}{3}$<x<3时,过点E作ED⊥FH的延长线于D,
动点C在线段AB上从点A向点B运动时,DF的长增大,故Rt△DEF中,EF的长增大;
综上所述,线段EF长度的变化情况是先减小后增大.
故选(D)
点评 本题主要考查了反比例函数图象上点的坐标特征,解决问题的关键是根据直角三角形的三边关系进行判断,解题时注意分类思想的运用.


科目:初中数学 来源: 题型:解答题
 如图,请你在钟面上画出时针和分针,使时针和分针互相垂直,并且此时表示的时间恰好是整点.
如图,请你在钟面上画出时针和分针,使时针和分针互相垂直,并且此时表示的时间恰好是整点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小于8km/h | B. | 大于8km/h | C. | 小于4km/h | D. | 大于4km/h |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+a,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2×(2-5)+2=2×(-3)+2=-6+2=4.
定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+a,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2×(2-5)+2=2×(-3)+2=-6+2=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 长方形一边的长a/cm | 6 | 8 | 10 | 12 | 14 | 16 |
| 长方形的面积/cm2 | 84 | 96 | 100 | 96 | 84 | 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,已知∠A=∠ABD,CD=1,AD=2,则
如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,已知∠A=∠ABD,CD=1,AD=2,则查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一个正方体的展开图,标注了字母“a”的面是正方体的正面,已知正方体相对两个面上的代数式的值相等.求a+$\sqrt{x+y}$的值.
如图是一个正方体的展开图,标注了字母“a”的面是正方体的正面,已知正方体相对两个面上的代数式的值相等.求a+$\sqrt{x+y}$的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com