考点:待定系数法求二次函数解析式,二次函数的性质
专题:计算题
分析:(1)根据抛物线的对称性得到B点坐标,则可设交点式y=a(x+2)(x-4),再把(0,4)代入可计算出a的值,从而得到抛物线解析式,然后写出a、b、c的值;
(2)把(1)的解析式配成顶点式即可得到M点的坐标;
(3)根据三角形面积公式求解.
解答:
解:∵抛物线的对称轴为直线x=1,
而A点坐标为(-2,0),
∴B点坐标为(4,0),
设抛物线解析式为y=a(x+2)(x-4),
把(0,4)代入得a•2•(-4)=4,解得a=-
,
所以抛物线解析式为y=-
(x+2)(x-4)=-
x
2+x+4,
所以a=-
,b=1,c=4;
(2)y=-
x
2+x+4
=-
(x-1)
2+
,
所以M点坐标为(1,
);
(3)△AMB的面积=
•(4+2)•
=
.
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质.

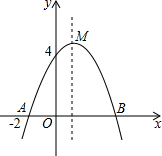 已知二次函数y=ax2+bx+c的图象如图的所示.
已知二次函数y=ax2+bx+c的图象如图的所示. 解:∵抛物线的对称轴为直线x=1,
解:∵抛物线的对称轴为直线x=1,

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案 如图,某大桥有一段抛物线型的拱梁,抛物线的表达式是y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶8秒时和28秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需
如图,某大桥有一段抛物线型的拱梁,抛物线的表达式是y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶8秒时和28秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需