Question

【题目】问题提出

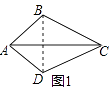
（1）如图①，已知△ABC，请画出△ABC关于直线AC对称的三角形．
问题探究
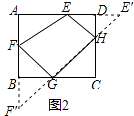
（2）如图②，在矩形ABCD中，AB=4，AD=6，AE=4，AF=2，是否在边BC、CD上分别存在点G、H，使得四边形EFGH的周长最小？若存在，求出它周长的最小值；若不存在，请说明理由．
问题解决
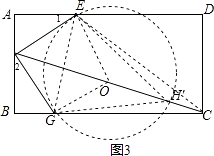
（3）如图③，有一矩形板材ABCD，AB=3米，AD=6米，现想从此板材中裁出一个面积尽可能大的四边形EFGH部件，使∠EFG=90°，EF=FG= 米，∠EHG=45°，经研究，只有当点E、F、G分别在边AD、AB、BC上，且AF＜BF，并满足点H在矩形ABCD内部或边上时，才有可能裁出符合要求的部件，试问能否裁得符合要求的面积尽可能大的四边形EFGH部件？若能，求出裁得的四边形EFGH部件的面积；若不能，请说明理由．

Answer 1

【答案】
（1）

解：如图1，△ADC即为所求；

（2）

解：存在，理由：作E关于CD的对称点E′，

作F关于BC的对称点F′，

连接E′F′，交BC于G，交CD于H，连接FG，EH，

则F′G=FG，E′H=EH，则此时四边形EFGH的周长最小，

由题意得：BF′=BF=AF=2，DE′=DE=2，∠A=90°，

∴AF′=6，AE′=8，

∴E′F′=10，EF=2 ，

∴四边形EFGH的周长的最小值=EF+FG+GH+HE=EF+E′F′=2 +10，

∴在边BC、CD上分别存在点G、H，

使得四边形EFGH的周长最小，

最小值为2 +10；

（3）

解：能裁得，

理由：∵EF=FG= ，∠A=∠B=90°，∠1+∠AFE=∠2+AFE=90°，

∴∠1=∠2，

在△AEF与△BGF中， ，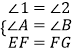

∴△AEF≌△BGF，

∴AF=BG，AE=BF，设AF=x，则AE=BF=3﹣x，

∴x2+（3﹣x）2=（ ）2，解得：x=1，x=2（不合题意，舍去），

∴AF=BG=1，BF=AE=2，

∴DE=4，CG=5，

连接EG，

作△EFG关于EG的对称△EOG，

则四边形EFGO是正方形，∠EOG=90°，

以O为圆心，以EG为半径作⊙O，

则∠EHG=45°的点在⊙O上，

连接FO，并延长交⊙O于H′，则H′在EG的垂直平分线上，

连接EH′GH′，则∠EH′G=45°，

此时，四边形EFGH′是要想裁得符合要求的面积最大的，

∴C在线段EG的垂直平分线设，

∴点F，O，H′，C在一条直线上，

∵EG= ，

∴OF=EG= ，

∵CF=2 ，

∴OC= ，

∵OH′=OE=FG= ，

∴OH′＜OC，

∴点H′在矩形ABCD的内部，

∴可以在矩形ABCD中，裁得符合条件的面积最大的四边形EFGH′部件，

这个部件的面积= EGFH′= × ×（ + ）=5+ ，

∴当所裁得的四边形部件为四边形EFGH′时，裁得了符合条件的最大部件，这个部件的面积为（5+ ）m2．

【解析】本题考查了全等三角形的判定和性质，矩形的性质，勾股定理，轴对称的性质，存在性问题，掌握的作出辅助线利用对称的性质解决问题是解题的关键．（1）作B关于AC 的对称点D，连接AD，CD，△AC即为所求；（2）作E关于CD的对称点E′，作F关于BC的对称点F′，连接E′F′，得到此时四边形EFGH的周长最小，根据轴对称的性质得到BF′=BF=AF=2，DE′=DE=2，∠A=90°，于是得到AF′=6，AE′=8，求出E′F′=10，EF=2 即可得到结论；（3）根据余角的性质得到1=∠2，推出△AEF≌△BGF，根据全等三角形的性质得到AF=BG，AE=BF，设AF=x，则AE=BF=3﹣x根据勾股定理列方程得到AF=BG=1，BF=AE=2，作△EFG关于EG的对称△EOG，则四边形EFGO是正方形，∠EOG=90°，以O为圆心，以EG为半径作⊙O，则∠EHG=45°的点在⊙O上，连接FO，并延长交⊙O于H′，则H′在EG的垂直平分线上，连接EH′GH′，则∠EH′G=45°，于是得到四边形EFGH′是符合条件的最大部件，根据矩形的面积公式即可得到结论．