
【题目】如图1,已知AB∥CD,∠B=30°,∠D=120°; 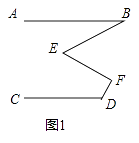
(1)若∠E=60°,则∠F=;
(2)请探索∠E与∠F之间满足的数量关系?说明理由;
(3)如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数. 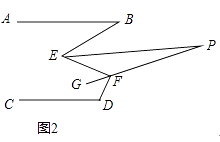
【答案】
(1)90°
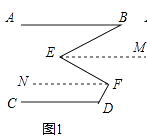
(2)解:如图1,分别过点E,F作EM∥AB,FN∥AB,
∴EM∥AB∥FN,
∴∠B=∠BEM=30°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=120°,
∴∠DFN=60°,
∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,
∴∠EFD=∠MEF+60°,
∴∠EFD=∠BEF+30°
(3)解:如图2,过点F作FH∥EP,
由(2)知,∠EFD=∠BEF+30°,
设∠BEF=2x°,则∠EFD=(2x+30)°,
∵EP平分∠BEF,GF平分∠EFD,
∴∠PEF= ![]() ∠BEF=x°,∠EFG=
∠BEF=x°,∠EFG= ![]() ∠EFD=(x+15)°,
∠EFD=(x+15)°,
∵FH∥EP,
∴∠PEF=∠EFH=x°,∠P=∠HFG,
∵∠HFG=∠EFG﹣∠EFH=15°,
∴∠P=15°
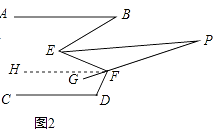
【解析】解:(1)如图1,分别过点E,F作EM∥AB,FN∥AB, ∴EM∥AB∥FN,
∴∠B=∠BEM=30°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=120°,
∴∠DFN=60°,
∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,
∴∠EFD=∠MEF+60°
∴∠EFD=∠BEF+30°=90°;
所以答案是:90°;
【考点精析】掌握平行线的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:
【题目】某电脑公司销售部为了定制下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是( )

A.19,20,14 B.19,20,20 C.18.4,20,20 D.18.4,25,20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区共有1800名初三学生,为解决这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
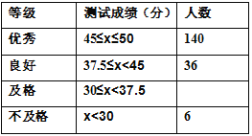
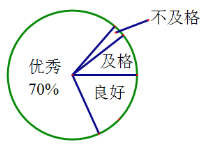
根据以上信息,解答下列问题:(1)本次测试学生体质健康成绩为良好的有_________人,达到优秀的人数占本次测试人数的百分比为____%.
(2)本次测试学生人数为_________人,其中,体质健康成绩为及格的有________人,不及格的人数占本次测试总人数的百分比是__________%.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空,并在括号内注明理由依据, 解:∵∠1=30°,∠2=30°
∴∠1=∠2
∴∥()
又AC⊥AE(已知)
∴∠EAC=90°
∴∠EAB=∠EAC+∠1=120°
同理:∠FBG=∠FBD+∠2=°.
∴∠EAB=∠FBG().
∴∥(同位角相等,两直线平行)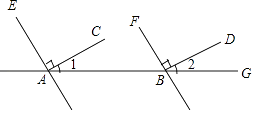
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°; 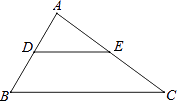
(1)求证:DE∥BC;
(2)求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为 . 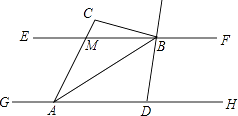
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com