
【题目】看图填空,并在括号内注明理由依据, 解:∵∠1=30°,∠2=30°
∴∠1=∠2
∴∥()
又AC⊥AE(已知)
∴∠EAC=90°
∴∠EAB=∠EAC+∠1=120°
同理:∠FBG=∠FBD+∠2=°.
∴∠EAB=∠FBG().
∴∥(同位角相等,两直线平行)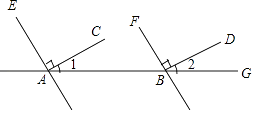
【答案】AC;BD;同位角相等,两直线平行;120;等式的性质;AE;BF
【解析】解:∵∠1=30°,∠2=30°, ∴∠1=∠2.
∴AC∥BD(同位角相等,两直线平行).
又∵AC⊥AE(已知),
∴∠EAC=90°(垂直定义 ),
∴∠EAB=∠EAC+∠1=120°.
同理:∠FBG=∠FBD+∠2=120°.
∴∠EAB=∠FBG(等式的性质).
∴AE∥BF(同位角相等,两直线平行).
所以答案是:AC,BD,同位角相等,两直线平行;120;等式的性质;AE,BF.
【考点精析】通过灵活运用平行线的判定与性质,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质即可以解答此题.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】若点A(-7,3)向右平移5个单位长度后得到点A',点B(4,-2)向左平移6个单位长度后得到点B',则A'B'所在的直线与x轴的关系是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知AB∥CD,∠B=30°,∠D=120°; 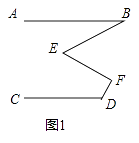
(1)若∠E=60°,则∠F=;
(2)请探索∠E与∠F之间满足的数量关系?说明理由;
(3)如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数. 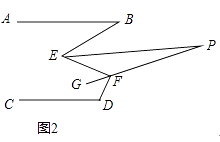
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2﹣2x﹣3上有两点:(﹣1,y1),(4,y2),下列结论正确的是( )
A.y1>y2B.y1<y2C.y1=y2D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com