
【题目】已知关于x的一元二次方程x22(k1)x+ k2+3=0的两实数根为x1,x2,设t=![]() ,则t的最大值为( )
,则t的最大值为( )
A.2B.2C.4D.4
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】植树节期间,某校360名学生参加植树活动,要求每人植树3~6棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:3棵;B:4棵;C:5棵;D:6棵.根据各类型对应的人数绘制了扇形统计图(如图1)和尚未完成的条形统计图(如图2).请解答下列问题:


(1)将条形统计图补充完整;
(2)这20名学生每人植树量的众数为________棵,中位数为________棵;
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的:
第一步:求平均数的公式是![]() ;
;
第二步:在该问题中,n=4,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
第三步:![]() .
.
①小宇的分析是不正确的,他错在第几步?
请你帮他计算出正确的平均数,并估计这360名学生共植树多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 、
、![]() 是反比例函数
是反比例函数![]()
![]() 图象上的点,
图象上的点,![]() 于点
于点![]() ,
,![]() .
.
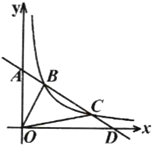
(1)求直线![]() 的函数解析式及反比例函数的解析式;
的函数解析式及反比例函数的解析式;
(2)若![]() 、
、![]() 、
、![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() ,
,![]() ,
,![]() 的一个数量关系式.
的一个数量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
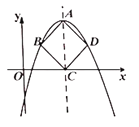
【题目】如图,抛物线![]() (
(![]() )的顶点为
)的顶点为![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() ,当以
,当以![]() 为对角线的正方形
为对角线的正方形![]() 的另外两个顶点
的另外两个顶点![]() 、
、![]() 恰好在抛物线上时,我们把这样的抛物线称为美丽抛物线,正方形
恰好在抛物线上时,我们把这样的抛物线称为美丽抛物线,正方形![]() 为它的内接正方形.
为它的内接正方形.
(1)当抛物线![]() 是美丽抛物线时,则
是美丽抛物线时,则![]() ______;当抛物线
______;当抛物线![]() 是美丽抛物线时,则
是美丽抛物线时,则![]() ______;
______;
(2)若抛物线![]() 是美丽抛物线时,则请直接写出
是美丽抛物线时,则请直接写出![]() ,
,![]() 的数量关系;
的数量关系;
(3)若![]() 是美丽抛物线时,(2)
是美丽抛物线时,(2)![]() ,
,![]() 的数量关系成立吗?为什么?
的数量关系成立吗?为什么?
(4)系列美丽抛物线![]() (
(![]() 为小于
为小于![]() 的正整数)顶点在直线
的正整数)顶点在直线![]() 上,且它们中恰有两条美丽抛物线内接正方形面积比为
上,且它们中恰有两条美丽抛物线内接正方形面积比为![]() .求它们二次项系数之和.
.求它们二次项系数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
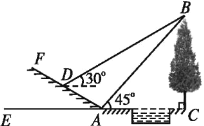
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是45°,若坡角∠FAE=30°,求大树的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
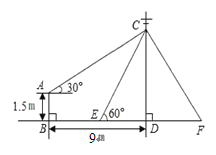
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆9m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )
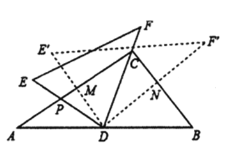
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输公司现将一批152吨的货物运往A,B两地,若用大小货车15辆,则恰好能一次性运完这批货.已知这两种大小货车的载货能力分别为12吨/辆和8吨/辆,其运往A,B两地的运费如下表所示:
目的地(车型) | A地(元/辆) | B地(元/辆) |
大货车 | 800 | 900 |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆.(用二元一次方程组解答)
(2)现安排其中的10辆货车前往A地,其余货车前往B地,设前往A地的大货车为x辆,前往A,B两地总费用为w元,试求w与x的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com