
 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线与BE的延长线相交于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线与BE的延长线相交于点F,连接CF.分析 (1)用一组对边平行且相等来得出四边形CDAF为平行四边形;
(2)构造直角三角形,判断出△ACD是等边三角形,得出特殊角,最后用锐角三角函数,勾股定理计算即可.
解答 解:(1)∵E是AD的中点,
∴AE=ED,
∵AF∥BC,
∴∠AFE=∠DBE,∠FAE=∠BDE,
∴△AFE≌△DBE,
∴AF=BD,
∵AD是BC边中线,
∴CD=BD,
∴AF=CD,
∴四边形CDAF是平行四边形,
(2)如图
过F点作FG⊥AB交BA的延长线于点G.
∵∠CAB=90°,AD是BC边中线,
∴AD=CD
又∵AC=AF,AF=CD,
∴AC=AD=CD,
∴△ACD是等边三角形,
∴∠ACB=60°,
∴∠ABC=30°,
又∵AF∥BC,
∴∠ABC=∠FAG=30°
∵AE=2,
∴AD=AC=AF=4,
∴在Rt△FAG和Rt△CAB中,
FG=FA×sin∠FAG=4sin30°=2,
AG=FA×cos∠FAG=4cos30°=2$\sqrt{3}$,
AB=AC×tan∠ACB=AC×tan60°=4$\sqrt{3}$,
∴GB=AG+BG=6$\sqrt{3}$
∴在Rt△FBG中,BF=$\sqrt{F{G}^{2}+G{B}^{2}}$=4$\sqrt{7}$.
点评 此题是平行四边形的性质和判定题,还考查等边三角形的判定和性质,锐角三角函数的意义,勾股定理,解本题的关键是得出∠ABC=30°,用锐角三角函数求线段的长是解本题的难点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 操作题
操作题查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有一张地图,有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,你能帮他确定C地的位置吗?
有一张地图,有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,你能帮他确定C地的位置吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
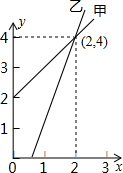 如图是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象,下列说法:
如图是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象,下列说法:| A. | ①② | B. | ②③ | C. | ①②④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
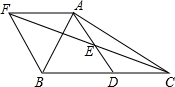 如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.
如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com