
 已知:点A、F、E、C在同一条直线上,AF=CE,BE∥DF,∠A=∠C.
已知:点A、F、E、C在同一条直线上,AF=CE,BE∥DF,∠A=∠C.分析 求出AE=CF,根据平行线的性质求出∠AEB=∠CFD,然后根据ASA推出△ABE≌△CDF即可.
解答 证明:∵AF=CE,
∴AF+EF=CE+EF,
∴AE=CF,
∵BE∥DF,
∴∠AEB=∠CFD ( 两直线平行,内错角相等 ),
在△ABE和△CDF中
$\left\{\begin{array}{l}{∠A=∠C}\\{AE=CF}\\{∠AEB=∠CFD}\end{array}\right.$
∴△ABE≌△CDF (ASA).
点评 本题考查的是全等三角形的判定,判定两个三角形全等,先根据求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.


科目:初中数学 来源: 题型:选择题
| A. | (6,-7)或(-6,-7) | B. | (-6,7)或(-6,-7) | C. | (6,7)或(-6,-7) | D. | (6,7)或(6,-7) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )| A. | SAS | B. | ASA | C. | SSS | D. | AAS |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数1.7与1.70表示的意义不同 | B. | 近似数0.03080有4个有效数字 | ||
| C. | 49553精确到万位是4.9×104 | D. | 5.230×104是精确到十位的近似数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 73 | B. | 150 | C. | $\frac{150}{73}$ | D. | $\frac{73}{150}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
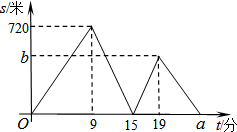 小宁、小波从学校出发到青少年宫参加书法比赛,小宁步行一段时间后,小波骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小宁出发时间t(分)之间的函数关系如图所示.下列说法:①小波先到达青少年宫;②小波的速度是小宁速度的2.5倍;③a=25;④b=460.其中正确的是( )
小宁、小波从学校出发到青少年宫参加书法比赛,小宁步行一段时间后,小波骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小宁出发时间t(分)之间的函数关系如图所示.下列说法:①小波先到达青少年宫;②小波的速度是小宁速度的2.5倍;③a=25;④b=460.其中正确的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com