
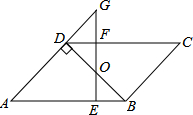
 如图,?ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
如图,?ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
|

| DF2+FG2 |
| 2 |
| AD |
| DG |
| EF |
| FG |
| AD | ||
|
| 2 |
| 1 |
| 2 |


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
| A、对角线相等是矩形具有而菱形不具有的性质 |
| B、对角线互相垂直平分是正方形具有而菱形不具有的性质 |
| C、每一条对角线平分一组对角是菱形具有而矩形不具有的性质 |
| D、顺次连接任意四边形各边中点所得的四边形一定是平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
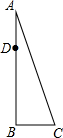 如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC滑到C处,另一只猴子从D处滑到地面B处,再由B处跑到C处,已知两猴子所经路程都是15m.
如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC滑到C处,另一只猴子从D处滑到地面B处,再由B处跑到C处,已知两猴子所经路程都是15m.查看答案和解析>>
科目:初中数学 来源: 题型:
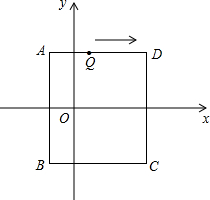 如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴.如果A点坐标是(-1,2
如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴.如果A点坐标是(-1,2| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
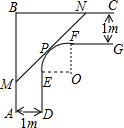 一走廊拐角的横截面积如图所示,已知AB⊥BC,AB∥DE,BC∥FG,且两组平行墙壁间的走廊宽度都是1m,
一走廊拐角的横截面积如图所示,已知AB⊥BC,AB∥DE,BC∥FG,且两组平行墙壁间的走廊宽度都是1m, |
| EF |
 |
| EF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com