
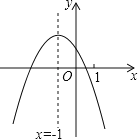
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】试题解析:∵抛物线和x轴有两个交点,
∴b2-4ac>0,
∴4ac-b2<0,∴①正确;
∵对称轴是直线x=-1,和x轴的一个交点在点(0,0)和点(1,0)之间,
∴抛物线和x轴的另一个交点在(-3,0)和(-2,0)之间,
∴把(-2,0)代入抛物线得:y=4a-2b+c>0,
∴4a+c>2b,∴②错误;
∵把x=1代入抛物线得:y=a+b+c<0,
∴2a+2b+2c<0,
∵-![]() =-1,
=-1,
∴b=2a,
∴3b+2c<0,∴③正确;
∵抛物线的对称轴是直线x=-1,
∴y=a-b+c的值最大,
即把x=m(m≠-1)代入得:y=am2+bm+c<a-b+c,
∴am2+bm+b<a,
即m(am+b)+b<a,∴④正确;
即正确的有3个,
故选B.


科目:初中数学 来源: 题型:
【题目】完成下列推理说明: 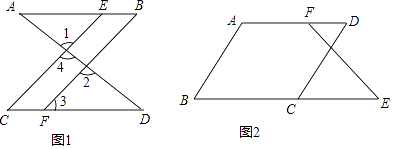
(1)如图1,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下: 因为∠1=∠2(已知),且∠1=∠4()
所以∠2=∠4(等量代换)
所以CE∥BF()
所以∠=∠3()
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD()
(2)如图2,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE. 证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD ()
∴∠B=()
又∵∠B=∠D(已知),
∴∠=∠(等量代换)
∴AD∥BE()
∴∠E=∠DFE()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用全面调查(普查)方式的是
A. 为了了解生产的一批炮弹的杀伤半径 B. 了解《人们的名义》反腐剧的收视率
C. 调查梅岭中学某班学生喜欢上数学课的情况 D. 调查某类烟花爆竹燃放的安全情况
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com