解:(1)当m=0时,原方程化为x+3=0,此时方程有实数根 x=-3.
当m≠0时,原方程为一元二次方程.
∵△=(3m+1)
2-12m=9m
2-6m+1=(3m-1)
2≥0.
∴此时方程有两个实数根.
综上,不论m为任何实数时,方程 mx
2+(3m+1)x+3=0总有实数根.
(2)∵令y=0,则 mx
2+(3m+1)x+3=0.
解得 x
1=-3,

.
∵抛物线y=mx
2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数,
∴m=1.
∴抛物线的解析式为y=x
2+4x+3.
(3)∵点P(x
1,y
1)与Q(x
1+n,y
2)在抛物线上,
∴
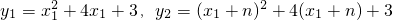
.
∵y
1=y
2,
∴
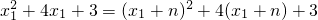
.
可得
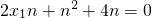
.
即 n(2x
1+n+4)=0.
∵点P,Q不重合,
∴n≠0.
∴2x
1=-n-4.
∴
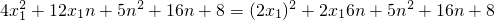
=(n+4)
2+6n(-n-4)+5n
2+16n+8=24.
分析:(1)分别讨论当m=0和m≠0的两种情况,分别对一元一次方程和一元二次方程的根进行判断;
(2)令y=0,则 mx
2+(3m+1)x+3=0,求出两根,再根据抛物线y=mx
2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数,求出m的值;
(3)点P(x
1,y
1)与Q(x
1+n,y
2)在抛物线上,求出y
1和y
2,y
1和y
2相等,求出 n(2x
1+n+4)=0,然后整体代入求出代数式的值.
点评:本题主要考查二次函数的综合题的知识,解答本题的关键熟练掌握方程与函数之间的联系,此题难度不大,第三问需要整体代入.

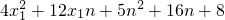 的值.
的值. .
.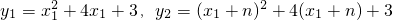 .
.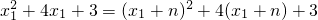 .
.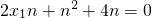 .
.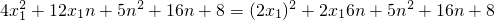 =(n+4)2+6n(-n-4)+5n2+16n+8=24.
=(n+4)2+6n(-n-4)+5n2+16n+8=24.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案