
分析 根据二元一次方程组的解法即可求出答案
解答 解:(1)①+②得:x=-1
把x=-1代入①得:y=2
∴原方程组的解为$\left\{\begin{array}{l}x=-1\\ y=2\end{array}\right.$
(2)原方程组化为:$\left\{\begin{array}{l}{x+2y=8①}\\{2x-y=1②}\end{array}\right.$
②×2+①得:x=2
将x=2代入②得y=3
所以该方程组的解为:$\left\{{\begin{array}{l}{x=2}\\{y=3}\end{array}}\right.$
点评 本题考查二元一次方程组,解题的关键是熟练运用二元一次方程组的解法,本题属于基础题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
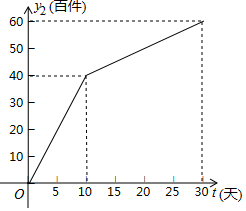 我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.| 时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量 y1(百件) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2与-$\frac{1}{2}$ | B. | 2与|-2| | C. | -2与$\root{3}{-8}$ | D. | -2与$\sqrt{(-2)^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-3x+2 | B. | y=-3x-2 | C. | y=-3(x+2) | D. | y=-3(x-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com