
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象分别交x轴、y轴于A、B两点,与反比例函数
的图象分别交x轴、y轴于A、B两点,与反比例函数 的图象交于C、D两点,DE⊥x轴于点E。已知C点的坐标是(6,
的图象交于C、D两点,DE⊥x轴于点E。已知C点的坐标是(6, ),AE=6,tan∠DAE=
),AE=6,tan∠DAE=

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
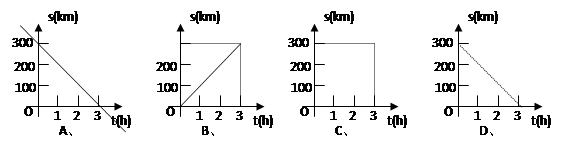
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 (单位:米)与车速
(单位:米)与车速 (单位:米/秒)之间有如下关系:
(单位:米/秒)之间有如下关系: 其中
其中 为司机的反应时间(单位: 秒),
为司机的反应时间(单位: 秒), 为制动系数.某机构为测试司机饮酒后刹车距离的变化,对某种型号的汽车进行了“醉汉”驾车测试,已知该型号汽车的制动系数
为制动系数.某机构为测试司机饮酒后刹车距离的变化,对某种型号的汽车进行了“醉汉”驾车测试,已知该型号汽车的制动系数 =0.1,并测得志愿者在未饮酒时的反应时间
=0.1,并测得志愿者在未饮酒时的反应时间 =0.5秒
=0.5秒查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
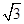 x-6
x-6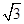 ,分别与x 轴y轴相交于A、B 两点.动点C从点B出发沿射线BA以3cm/秒的速度运动,以C点为圆心作半径为1cm的⊙C.
,分别与x 轴y轴相交于A、B 两点.动点C从点B出发沿射线BA以3cm/秒的速度运动,以C点为圆心作半径为1cm的⊙C.
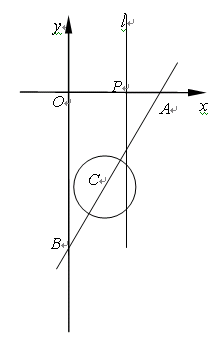
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (千克)与销售单价
(千克)与销售单价 (元)之间存在一次函数关系.求
(元)之间存在一次函数关系.求 (千克)与
(千克)与 (元)(
(元)( )的函数关系式;(6分)
)的函数关系式;(6分)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com