
|


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 线BD上.若AB=6m,AD=4m,设AM的长为xm,矩形AMPQ的面积为S平方米.
线BD上.若AB=6m,AD=4m,设AM的长为xm,矩形AMPQ的面积为S平方米.查看答案和解析>>
科目:初中数学 来源: 题型:
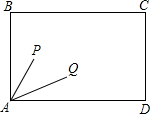
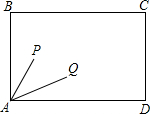 在台球桌矩形,ABCD上,放有两个球P和Q,恰有∠PAB和∠QAD相等.如果打击球P使它撞在AB的M点反弹后撞到球Q,其路线记为P→M→Q;如果打击球 Q,使它撞在AD的N点反弹后撞到球P,其路线记为Q→N→P.证明:P→M→Q与Q→N→P的路线长相等.
在台球桌矩形,ABCD上,放有两个球P和Q,恰有∠PAB和∠QAD相等.如果打击球P使它撞在AB的M点反弹后撞到球Q,其路线记为P→M→Q;如果打击球 Q,使它撞在AD的N点反弹后撞到球P,其路线记为Q→N→P.证明:P→M→Q与Q→N→P的路线长相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
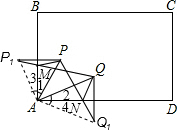
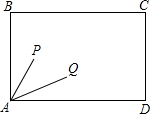 在台球桌矩形,ABCD上,放有两个球P和Q,恰有∠PAB和∠QAD相等.如果打击球P使它撞在AB的M点反弹后撞到球Q,其路线记为P→M→Q;如果打击球 Q,使它撞在AD的N点反弹后撞到球P,其路线记为Q→N→P.证明:P→M→Q与Q→N→P的路线长相等.
在台球桌矩形,ABCD上,放有两个球P和Q,恰有∠PAB和∠QAD相等.如果打击球P使它撞在AB的M点反弹后撞到球Q,其路线记为P→M→Q;如果打击球 Q,使它撞在AD的N点反弹后撞到球P,其路线记为Q→N→P.证明:P→M→Q与Q→N→P的路线长相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com