
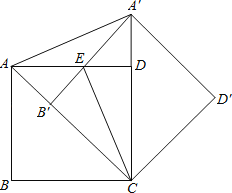
【题目】如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.
求证:(1)△ADA′≌△CDE;
(2)直线CE是线段AA′的垂直平分线.
【答案】证明:(1)∵四边形ABCD是正方形,∴AD=CD,∠ADC=90°。∴∠A′DE=90°。
根据旋转的方法可得:∠EA′D=45°,∴∠A′ED=45°。∴A′D=DE。
∵在△AD A′和△CDE中,AD=CD,∠EDC=∠A′DA=90°,A′D=DE,
∴△ADA′≌△CDE(SAS)。
(2)∵AC=A′C,∴点C在AA′的垂直平分线上。
∵AC是正方形ABCD的对角线,∴∠CAE=45°。
∵AC=A′C,CD=CB′,∴AB′=A′D。
∵在△AEB′和△A′ED中,∠EAB′=∠EA′D,∠AEB′=∠A′ED,AB′=A′D,
∴△AEB′≌△A′ED(AAS)。∴AE=A′E。
∴点E也在AA′的垂直平分线上。∴直线CE是线段AA′的垂直平分线。
【解析】正方形的性质,旋转的性质,等腰三角形的判定,全等三角形的判定和性质,线段垂直平分线的判定。


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某超市准备购进A、B两种品牌台灯,其中A每盏进价比B进价贵30元,A售价120元,B售价80元.已知用1040元购进的A数量与用650元购进B的数量相同.
(1)求A、B的进价;
(2)超市打算购进A、B台灯共100盏,要求A、B的总利润不得少于3400元,不得多于3550元,问有多少种进货方案?
(3)在(2)的条件下,该超市决定对A进行降价促销,A台灯每盏降价m(8<m<15)元,B不变,超市如何进货获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.三角形三条角平分线的交点叫重心
B.三角形三条高交于一点
C.面积相等的两个三角形一定全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
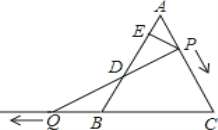
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
求证:∠A=∠F.

证明:∵∠AGB=∠EHF
∠AGB=___________(对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC(____________________________________)
∴∠_________=∠DBA(________________________________)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥_______(__________________________________)
∴∠A=∠F(__________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(6,0),(0,10),点B在第一象限内.
(1)写出点B的坐标,并求长方形OABC的周长;
(2)若有过点C的直线CD把长方形OABC的周长分成3:5两部分,D为直线CD与长方形的边的交点,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查方式,你认为最合适的是( )
A.日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式
B.旅客上飞机前的安检,采用抽样调查方式
C.了解深圳市居民日平均用水量,采用全面调查方式
D.了解深圳市每天的平均用电量,采用抽样调查方式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com