
【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( ) 
A.![]()
B.6
C.![]()
D.![]()
【答案】A
【解析】解:连接BC′, 
∵旋转角∠BAB′=45°,∠BAD′=45°,
∴B在对角线AC′上,
∵B′C′=AB′=3,
在Rt△AB′C′中,AC′= ![]() =3
=3 ![]() ,
,
∴BC′=3 ![]() ﹣3,
﹣3,
在等腰Rt△OBC′中,OB=BC′=3 ![]() ﹣3,
﹣3,
在直角三角形OBC′中,OC′= ![]() (3
(3 ![]() ﹣3)=6﹣3
﹣3)=6﹣3 ![]() ,
,
∴OD′=3﹣OC′=3 ![]() ﹣3,
﹣3,
∴四边形ABOD′的周长是:2AD′+OB+OD′=6+3 ![]() ﹣3+3
﹣3+3 ![]() ﹣3=6
﹣3=6 ![]() .
.
故选:A.
由边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,利用勾股定理的知识求出BC′的长,再根据等腰直角三角形的性质,勾股定理可求BO,OD′,从而可求四边形ABOD′的周长.


科目:初中数学 来源: 题型:
【题目】中学生骑电动车上学的现象越来越受到社会的关注.为此某媒体记者小李随机调查了城区若干名中学生家长对这种现象的态度(态度分为:A:无所谓;B:反对;C:赞成)并将调査结果绘制成图①和图②的统计图(不完整)请根据图中提供的信息,解答下列问题:
(1)此次抽样调査中.共调査了名中学生家长;
(2)将图①补充完整;
(3)根据抽样调查结果.请你估计我市城区80000名中学生家长中有多少名家长持反对态度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,边长为2的正方形ABCD中,E是BA延长线上一点,且AE=AB,点P从点D出发,以每秒1个单位长度沿D→CB向终点B运动,直线EP交AD于点F,过点F作直线FG⊥DE于点G,交AB于点R.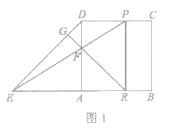

(1)求证:AF=AR;
(2)设点P运动的时间为t秒,求当选t为何值时,四边形PRBC是矩形?
(3)如图2,连接PB,请直线写出使△PRB是等腰三角形时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
A.x﹣y2=3
B.2x﹣y2=9
C.3x﹣y2=15
D.4x﹣y2=21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径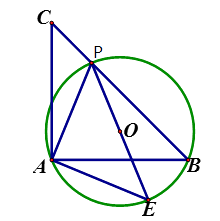
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 ![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题. 
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至点E,使得OE=OB,交⊙O于点F,连接AE,CE. 
(1)求证:AE是⊙O的切线;
(2)求证:四边形ADCE是矩形;
(3)若BD= ![]() AD=4,求阴影部分的面积.
AD=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小梅家的阳台上放置了一个晒衣架如图1,图2是晒衣架的侧面示意图,A,B两点立于地面,将晒衣架稳固张开,测得张角∠AOB=62°,立杆OA=OB=140cm,小梅的连衣裙穿在衣架后的总长度为122cm,问将这件连衣裙垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com