
【题目】如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
A.x﹣y2=3
B.2x﹣y2=9
C.3x﹣y2=15
D.4x﹣y2=21
【答案】B
【解析】解: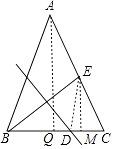
过A作AQ⊥BC于Q,过E作EM⊥BC于M,连接DE,
∵BE的垂直平分线交BC于D,BD=x,
∴BD=DE=x,
∵AB=AC,BC=12,tan∠ACB=y,
∴ ![]() =
= ![]() =y,BQ=CQ=6,
=y,BQ=CQ=6,
∴AQ=6y,
∵AQ⊥BC,EM⊥BC,
∴AQ∥EM,
∵E为AC中点,
∴CM=QM= ![]() CQ=3,
CQ=3,
∴EM=3y,
∴DM=12﹣3﹣x=9﹣x,
在Rt△EDM中,由勾股定理得:x2=(3y)2+(9﹣x)2 ,
即2x﹣y2=9,
故选B.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作第三个正方形AEGH,如此下去….若正方形ABCD的边长记为a1 , 按上述方法所作的正方形的边长依次为a2 , a3 , a4 , …,an , 则an= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的对角线相交于点O,M、N分别是OD、OC上异于O、C、D的点. 
(1)请你在下列条件①DM=CN,②OM=ON,③MN是△OCD的中位线,④MN∥AB中任选一个添加条件(或添加一个你认为更满意的其他条件),使四边形ABNM为等腰梯形,你添加的条件是 .
(2)添加条件后,请证明四边形ABNM是等腰梯形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在□ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
(1)求证:OE=OF;
(2)若AB=6,BC=5,OE=2,求四边形BCFE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健向器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。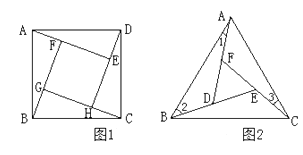
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设 ![]() ,
, ![]() ,
, ![]() ,请探索
,请探索 ![]() ,
, ![]() ,
, ![]() 满足的等量关系。
满足的等量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( ) 
A.![]()
B.6
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(精确到0.1)(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.132)
≈1.132)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个数字游戏:将1,2,3,4,5,6,7,8,9这九个数字分别填在如图所示的九个空格中,要求每一行从左到右的数字逐渐增大,每一列从上到下的数字也逐渐增大.当数字3和4固定在图中所示的位置时,x代表的数字是 , 此时按游戏规则填写空格,所有可能出现的结果共有种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com