练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．若△ABC∽△DEF，且∠A=70°，∠B=60°则∠D=70°，∠F=50°．

    分析 先利用三角形内角和计算出∠C的度数，然后根据相似三角形的性质求解．

    解答 解：∵∠A=70°，∠B=60°，
    ∴∠C=50°，
    ∵△ABC∽△DEF，
    ∴∠D=∠A=70°，∠F=∠C=50°．
    故答案为70°，50°．

    点评 本题考查了相似三角形的性质：相似三角形的对应角相等，对应边的比相等；相似三角形（多边形）的周长的比等于相似比．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

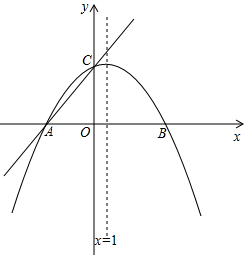    11．如图，在平面直角坐标系xOy中，一次函数y=$\frac{5}{4}$x+m（m为常数）的图象与x轴交于点A（-3，0），与y轴交于点C，以直线x=1为对称轴的抛物线y=ax2+bx+c（a、b、c为常数，且a≠0）经过A、C两点，并与x轴的正半轴交于点B
    （1）求m的值及抛物线的函数表达式；
    （2）是否存在抛物线上一动点Q，使得△ACQ是以AC为直角边的直角三角形？若存在，求出点Q的横坐标；若存在，请说明理由；
    （3）若P是抛物线对称轴上一动点，且使△ACP周长最小，过点P任意作一条与y轴不平行的直线交抛物线于M1（x1，y1），M2（x2，y2）两点，试问$\frac{{M}_{1}P•{M}_{2}P}{{M}_{1}{M}_{2}}$是否为定值，如果是，请求出结果，如果不是请说明理由．
    （参考公式：在平面直角坐标之中，若A（（x1，y1），B（x2，y2），则A，B两点间的距离为AB=${\sqrt{（{x}_{1}-{x}_{2}）^{2}+（{y}_{1}-{y}_{2}）^{2}}}^{\;}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．因式分解法解下列方程
    （1）x2-4=0；（2）（x+1）2-25=0
    （3）（x+2）（x-4）=0；（4）5x2=4x
    （5）x-2=x（x-2）；（6）4x（2x+1）=3（2x+1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．因式分解：36x2-12xy+y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，使AE=CF，连接AF，BE相交于点P．
    （1）求证：AF=BE，并求∠APB的度数；
    （2）若AE=2，试求AP•AF的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．请从以下两个小题中任选一个作答，若多选，则按第一题计分．
    A．一个多边形的每个内角都等于150°，则这个多边形是十二边形．
    B．用计算器计算：sin15°32'=0.27（精确到0.01）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

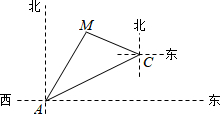    19．如图，某天然气公司的主输气管道从A市的北偏东60°方向直线延伸，测绘员在A处测得要安装天然气的M小区在A市北偏东30°方向，测绘员沿主输气管道步行2000米到达C处，测得小区M位于C的北偏西75°方向，请你在主输气管道上寻找支管道连接点N，使到该小区铺设的管道最短，并求出管道MN的长度（精确到0.1米）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图，正方形ABCD的边长为10，AG=CH=8，BG=DH=6，连接GH，则线段GH的长为2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，已知∠ACB=90°，且AC=BC，AD⊥CD，BE⊥CD，垂足分别为D、E，求证：CD=BE．

    查看答案和解析>>

    同步练习册答案