练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．利用平方差公式计算：（1+$\frac{1}{2}$）×（1+$\frac{1}{4}$）×（1+$\frac{1}{16}$）

    分析 乘上2×（1-$\frac{1}{2}$），逐步利用平方差公式计算得出答案即可．

    解答 解：原式=2×（1-$\frac{1}{2}$）×（1+$\frac{1}{2}$）×（1+$\frac{1}{4}$）×（1+$\frac{1}{16}$）
    =2×（1-$\frac{1}{4}$）×（1+$\frac{1}{4}$）×（1+$\frac{1}{16}$）
    =2×（1-$\frac{1}{16}$）×（1+$\frac{1}{16}$）
    =2×（1-$\frac{1}{256}$）
    =2×$\frac{255}{256}$
    =$\frac{255}{128}$．

    点评 此题考查平方差公式，掌握平方差公式（a+b）（a-b）=a2-b2，是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．三角形是最基本的图形，每个多边形都可以按不同的方式分割成若干个三角形，如下图，请按下列提示总结规律
    （1）如图①所示，从n边形一个顶点出发，分别连接这个顶点与其余各点（相邻顶点除外），可把这个n边形分割成n-2三角形；
    （2）如图②，从n边形一边上任意一点（顶点除外）出发，分别连接这个点与其余各顶点（左右相邻顶点除外），可把这个n边形分割成n-1个三角形；
    （3）如图③，从n边形内部任意一点出发，分别连接这个点与各顶点，可把这个n边形分割成n个三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．当m为何值时，关于x的方程（m+1）x|m-1|+（m-3）x=5．
    （1）为一元二次方程；
    （2）为一元一次方程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．当x=3时，5（x-4a）的值比3（x-a）的值的2倍少1，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知a3m•a2n=a7，a3m÷a2n=a5，求mn的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．当m=3时，ab|m|+（m+3）a2-3是四次三项式，这个多项式按a的升幂排列是6a2+ab3-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．根据下列条件，分别求出对应的二次函数的表达式．
    （1）已知二次函数的图象经过点（0，2）、（1，1）、（3，5）；
    （2）已知抛物线的顶点为（-1，2），且过点（2，1）；
    （3）已知抛物线与x轴交于点M（-3，0）、（5、0），且与y轴交于点（0，-3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，在四边形ABCD中，AD∥BC，AD=12，CD=10，BC=20，高DE=8，点P从点A出发，沿A-D-A运动，点Q从点C出发，沿CB方向运动，速度均为每秒4个单位长度．P、Q两点同时出发，当点Q到达B点时，P、Q两点同时停止运动．设点P运动时间为t（秒），连接P、Q．
    （1）当t=1时，AP=4；当t=4时，AP=8
    （2）连接DQ，在整个运动过程中，当t为何值时，△DPQ的面积为24？
    （3）设点C、D关于直线PQ的对称点分别为点C′、D′，直接写出C′D′∥BC时所有t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

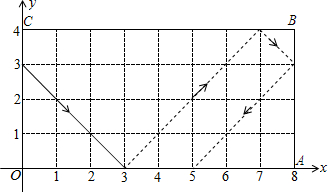    15．如图，动点P从（0，3）出发，沿所示方向运动，每当碰到长方形OABC的边时反弹，反弹后的路径与长方形的边的夹角为45°，第1次碰到长方形边上的点的坐标为（3，0），则第3次碰到长方形边上的点的坐标为（8，3），第2015次碰到长方形边上的点的坐标为（1，4）．

    查看答案和解析>>

    同步练习册答案