
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 2 |


| 2 |

查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(浙江衢州卷)数学(带解析) 题型:解答题
课本中,把长与宽之比为 的矩形纸片称为标准纸.请思考解决下列问题:
的矩形纸片称为标准纸.请思考解决下列问题:
(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明.
(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:
第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);
第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙),此时E点恰好落在AE边上的点M处;
第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.
请你探究:矩形纸片ABCD是否是一张标准纸?请说明理由.
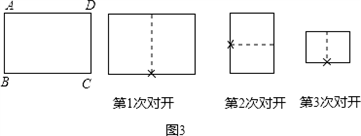
(3)不难发现:将一张标准纸按如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC= ,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏无锡市九年级第一学期期中考试数学试卷(解析版) 题型:解答题
课本中把长与宽之比为 的矩形纸片称为标准纸.请解决下列问题:
的矩形纸片称为标准纸.请解决下列问题:
(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明;

(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:
第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);
第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙) .此时E点恰好落在AE边上的点M处;
第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.

请你研究,矩形纸片ABCD是否是一张标准纸?请说明理由.
(3)不难发现,将一张标准纸如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC= ,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2002次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2002次对开后所得标准纸的周长.

查看答案和解析>>
科目:初中数学 来源:浙江省中考真题 题型:解答题
 的矩形纸片称为标准纸.请思考解决下列问题:
的矩形纸片称为标准纸.请思考解决下列问题: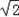 ,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.…
,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.…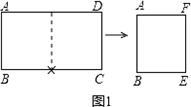
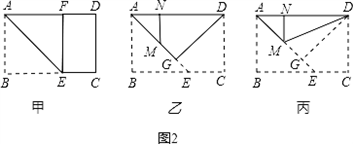
查看答案和解析>>
科目:初中数学 来源:2012年浙江省衢州市中考数学试卷(解析版) 题型:解答题
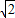 的矩形纸片称为标准纸.请思考解决下列问题:
的矩形纸片称为标准纸.请思考解决下列问题: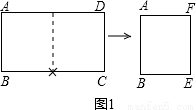
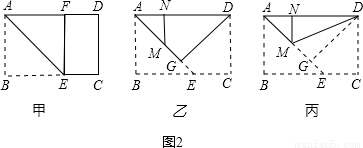
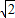 ,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com