
【题目】计算与解不等式组
(1)计算:|﹣2 ![]() |﹣4sin45°+(3﹣π)°﹣(
|﹣4sin45°+(3﹣π)°﹣( ![]() )﹣2;
)﹣2;
(2)解不等式组: 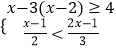 ,并在数轴上表示它的解集.
,并在数轴上表示它的解集.
【答案】
(1)解:原式=2 ![]() +1﹣9=﹣8
+1﹣9=﹣8
(2)解:解x﹣3(x﹣2)≥4得:x≤1;
解 ![]() 得:x>﹣1,
得:x>﹣1,
∴不等式组的解集为:﹣1<x≤1;
在数轴上表示如图所示:
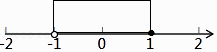
【解析】(1)利用二次根式的化简,特殊角的三角函数,零指数幂和负整数指数幂的运算法则运算即可;(2)求出两个不等式的解集,根据找不等式组解集的规律找出不等式组的解集即可.
【考点精析】本题主要考查了整数指数幂的运算性质和一元一次不等式组的解法的相关知识点,需要掌握aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数);解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市为了更有效地利用水资源,制定了居民用水收费标准:如果一户每月用水量不超过20立方米,每立方米按1.5元收费;如果超过20立方米,超过部分每立方米按1.8元收费,其余仍按每立方米1.5元计算,另外,超过的部分每立方米加收污水处理费1元,若某户一月份用水量![]() (
(![]() >20)立方米,问:
>20)立方米,问:
(1)该户一月份应交水费多少元?(请用含![]() 的代数式表示)
的代数式表示)
(2)该户三月份用水量为32立方米,请问该户三月份应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
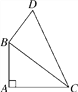
【题目】如图所示,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.
(1)连接BC,求BC的长;
(2)求四边形ABDC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石.某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:
收费 方式 | 月使用费(元) | 包时上网 时间(h) | 超时费(元/min) |
A | 7 | 25 | 0.6 |
B | 10 | 50 | 0.8 |
设小明每月上网学习人工智能课程的时间为x小时,方案A,B的收费金额分别为yA元,yB元.
(1)当x≥50时,分别求出yA,yB与x之间的函数关系式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在一张长方形纸条上画一条数轴.
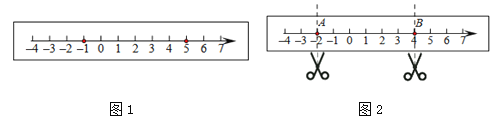
(1)折叠纸条使数轴上表示![]() 的点与表示5的点重合,折痕与数轴的交点表示的数是 ;
的点与表示5的点重合,折痕与数轴的交点表示的数是 ;
(2)如果数轴上两点之间的距离为8,经过(1)的折叠方式能够重合,那么左边这个点表示的数是 ;
(3)如图2,点A、B表示的数分别是![]() 、
、![]() ,数轴上有点C,使得AC=2BC,那么点C表示的数是 ;
,数轴上有点C,使得AC=2BC,那么点C表示的数是 ;
(4)如图2,若将此纸条沿A、B两处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折![]() 次后,再将其展开,求最左端的折痕与数轴的交点表示的数.(用含
次后,再将其展开,求最左端的折痕与数轴的交点表示的数.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
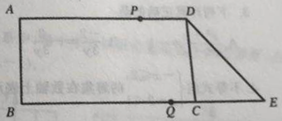
【题目】如图,在平行四边形ABCD中,∠B=90°,且AD=9cm,AB=4cm,延长BC到点E,使CE=3cm,连接DE.若动点P从A点出发,以每秒2cm的速度沿线段AD运动;动点Q从E点出发以每秒3cm的速度沿EB向B点运动,当点P、Q有一个到位置时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:
(1)求DE的长
(2)当t为多少时,四边形PQED成为平行四边形;
(3)请直接写出使得△DQE是等腰三角形时t的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)写出点A、B的坐标:
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).
(3)△ABC的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com