
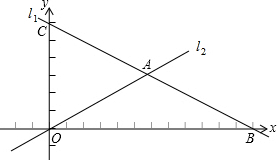
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��y=-$\frac{1}{2}$x+6�ֱ���x�ᡢy�ύ�ڵ�B��C������ֱ��l2��y=$\frac{1}{2}$x���ڵ�A��
��ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��y=-$\frac{1}{2}$x+6�ֱ���x�ᡢy�ύ�ڵ�B��C������ֱ��l2��y=$\frac{1}{2}$x���ڵ�A������ ��1������ֱ��l1����ʽ���ֱ���x��yΪ0���y��x��ֵ��ȷ����B��C�����꣬������ֱ�߽���ʽ���A�����꼴�ɣ�
��2������D��ֱ��OA�ϣ����D���꣬��ʾ��������COD���������֪����������x��ֵ��ȷ����D���꣬���ô���ϵ�������CD����ʽ���ɣ�
��3���ڣ�2���������£���P������CD�ϵĵ㣬��ƽ���ڴ��ڵ�Q��ʹ��O��C��P��QΪ������ı��������Σ���ͼ��ʾ��������������ǣ���i�����ı���OP1Q1CΪ����ʱ���ɡ�COP1=90�㣬�õ��ı���OP1Q1CΪ�����Σ���ii�����ı���OP2CQ2Ϊ����ʱ����iii�����ı���OQ3P3CΪ����ʱ���ֱ����Q���꼴�ɣ�
��� �⣺��1��ֱ��l1��y=-$\frac{1}{2}$x+6��
��x=0ʱ��y=6����y=0ʱ��x=12��
��B��12��0����C��0��6����
�ⷽ���飺$\left\{\begin{array}{l}{y=-\frac{1}{2}x+6}\\{y=\frac{1}{2}x}\end{array}\right.$�ã�$\left\{\begin{array}{l}{x=6}\\{y=3}\end{array}\right.$��
��A��6��3����
�ʴ�Ϊ����6��3������12��0������0��6����
��2����D��x��$\frac{1}{2}$x����
�ߡ�COD�����Ϊ12��
��$\frac{1}{2}$��6��x=12��
��ã�x=4��
��D��4��2����
��ֱ��CD�ĺ�������ʽ��y=kx+b��
��C��0��6����D��4��2������ã�$\left\{\begin{array}{l}{6=b}\\{2=4k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$��
��ֱ��CD����ʽΪy=-x+6��
��3�����ڵ�Q��ʹ��O��C��P��QΪ������ı��������Σ�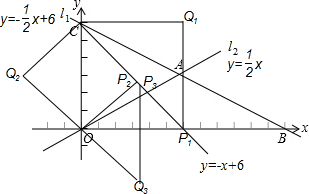
��ͼ��ʾ��������������ǣ�
��i�����ı���OP1Q1CΪ����ʱ���ɡ�COP1=90�㣬�õ��ı���OP1Q1CΪ�����Σ���ʱQ1P1=OP1=OC=6����Q1��6��6����
��ii�����ı���OP2CQ2Ϊ����ʱ����C����Ϊ��0��6�����õ�Q2������Ϊ3��
��y=3����ֱ��OQ2����ʽy=-x�У��ã�x=-3����ʱQ2��-3��3����
��iii�����ı���OQ3P3CΪ����ʱ������OQ3=OC=CP3=P3Q3=6����ʱQ3��3$\sqrt{2}$��-3$\sqrt{2}$����
���ϣ���Q�������ǣ�6��6����-3��3����3$\sqrt{2}$��-3$\sqrt{2}$����
���� ��������һ�κ����ۺ��⣬�漰��֪ʶ�У�һ�κ�����������Ľ��㣬����ϵ����ȷ��һ�κ�������ʽ��һ�κ���ͼ��Ľ��㣬һ�κ���ͼ�������ʣ����ε����ʣ�������ͼ�����ʣ��������մ���ϵ�����ǽⱾ��Ĺؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �� | B�� | �ڢ� | C�� | �٢� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
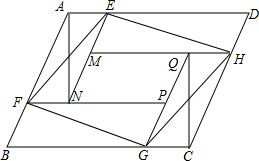 ��ͼ���а˸�ȫ�ȵ�������ƴ��һ�����ı���ABCD���м�һ��С�ı���MNPQ������EF��GH�õ��ı���EFGH����S�ı���ABCD=S1��S�ı���EFGH=S2��S�ı���MNPQ=S3����S1+S2+S3=10����S2=$\frac{10}{3}$��
��ͼ���а˸�ȫ�ȵ�������ƴ��һ�����ı���ABCD���м�һ��С�ı���MNPQ������EF��GH�õ��ı���EFGH����S�ı���ABCD=S1��S�ı���EFGH=S2��S�ı���MNPQ=S3����S1+S2+S3=10����S2=$\frac{10}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
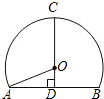 ��ͼ����������״����OΪԲ�ĵ�Բ��һ���֣�AB=8����CD=8����뾶OA����5��
��ͼ����������״����OΪԲ�ĵ�Բ��һ���֣�AB=8����CD=8����뾶OA����5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD�У���DAF=25�㣬AF���Խ���BD�ڵ�E������EC�����BCE=65�㣮
��ͼ��������ABCD�У���DAF=25�㣬AF���Խ���BD�ڵ�E������EC�����BCE=65�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
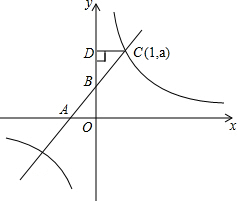 ��ͼ��ֱ��y=kx+2��x�ᡢy��ֱ��ڵ�A��B����C��1��a������E��b��-2����ֱ����˫����y=$\frac{m}{x}$���������㣬����C��CD��y�ᣬ����ΪD���ҡ�BCD�����Ϊ1��
��ͼ��ֱ��y=kx+2��x�ᡢy��ֱ��ڵ�A��B����C��1��a������E��b��-2����ֱ����˫����y=$\frac{m}{x}$���������㣬����C��CD��y�ᣬ����ΪD���ҡ�BCD�����Ϊ1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��-\right.2��2\sqrt{3}\left.{\;}��$ | B�� | $��-2��-2\sqrt{3}��$ | C�� | ��2$\sqrt{3}$��2�� | D�� | ��2��2�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com