
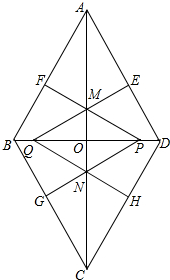
 菱形ABCD的对角线AC,BD相交于点O,AC=4
菱形ABCD的对角线AC,BD相交于点O,AC=4| 3 |
| 3 |
| 3 |
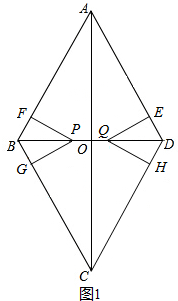 解:(1)①当点P在BO上,0<x≤2时,如图1所示.
解:(1)①当点P在BO上,0<x≤2时,如图1所示.| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| AO |
| BO |
| 3 |
| FP |
| BP |
| FP |
| x |
| ||
| 2 |
| ||
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| x |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| FM |
| AF |
| ||
| 3 |
| ||
| 3 |
| x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| ||
| 3 |
| x |
| 2 |
| ||
| 6 |
| x |
| 2 |
| ||
| 6 |
| x |
| 2 |
| ||
| 6 |
| 3 |
| 3 |
| ||
| 6 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| ||
| 6 |
| ||
| 6 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
| ||
| 6 |
| 3 |
| 6 |
| 6 |
| 6 |
| 6 |
| 6 |
| 6 |


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
 随着人民生活水平的提高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选一项):
随着人民生活水平的提高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选一项):| 管理措施 | 回答人数 | 百分比 |
| A | 25 | 5% |
| B | 100 | m |
| C | 75 | 15% |
| D | n | 35% |
| E | 125 | 25% |
| 合计 | a | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
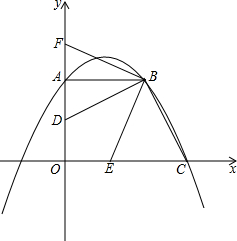 如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在第一象限,点C的坐标为(3,0).AB∥x轴,且OA=AB,抛物线y=ax2+bx+2经过点A、B、C.连 结BC,过点B作BD⊥BC,交OA于点D.将∠CBD绕点B按顺时针方向旋转得到∠EBF,角的两边分别交x轴的正半轴、y轴的正半轴于E、F.
如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在第一象限,点C的坐标为(3,0).AB∥x轴,且OA=AB,抛物线y=ax2+bx+2经过点A、B、C.连 结BC,过点B作BD⊥BC,交OA于点D.将∠CBD绕点B按顺时针方向旋转得到∠EBF,角的两边分别交x轴的正半轴、y轴的正半轴于E、F.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com