
在直角坐标平面中,已知点A(10,0)和点D(8,0).点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形.

(1)求C点坐标;
(2)求过O、C、B三点的抛物线解析式
(3)判断:(2)中抛物线的顶点与⊙M的位置关系,说明理由.
(1)点C的坐标为(1,3);(2)y=-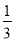 x2+
x2+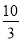 x,(3)抛物线的顶点在⊙M外.理由见解析.
x,(3)抛物线的顶点在⊙M外.理由见解析.
【解析】
试题分析:(1)作MN⊥BC于点N,连接MC,利用垂径定理求得线段MN后即可确定点C的坐标;
(2)用同样的方法确定点D的坐标后利用待定系数法确定二次函数的解析式,然后配方后即可确定抛物线的顶点坐标及对称轴;
(3)根据抛物线的顶点坐标和点M的坐标确定两点之间的距离,然后根据半径与两点之间的线段的大小关系即可确定顶点与圆的位置关系.
试题解析:(1)如图,作MN⊥BC于点N,连接MC,
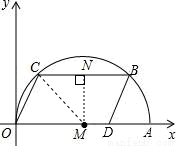
∵A(10,0)和点D(8,0).
∴点M(5,0),
∵点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形,
∴⊙M的半径为5,BC=OD=8,
∴在Rt△MNC中,MC=5,NC=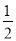 BC=4,
BC=4,
∴MN=3,
∴点C的坐标为(1,3);
(2)∵点C的坐标为(1,3),
∴点B的坐标为(9,3),
设过O、C、B三点的抛物线解析式为y=ax2+bx,
∴
解得:
∴解析式为:y=-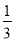 x2+
x2+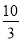 x,
x,
∴y=-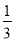 x2+
x2+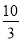 x =-
x =-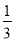 (x-5)2+
(x-5)2+ ,
,
∴对称轴为x=5,顶点坐标为(5, );
);
(3)∵顶点坐标为(5, ),点M的坐标为(5,0),
),点M的坐标为(5,0),
∴顶点到点M的距离为 ,
,
∵ >5
>5
∴抛物线的顶点在⊙M外.
考点:二次函数综合题.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源:2013-2014学年福建省南平市中考模拟数学试卷(解析版) 题型:解答题
(1)计算:2sin30°+(﹣1)2﹣|2﹣ |
|
(2)解方程:x2+2x﹣2=0。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:①2a﹣b<0;②abc<0;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c>0,错误的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
如图,点B在反比例函数y=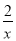 (x>0)的图象上,过点B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为( )
(x>0)的图象上,过点B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为( )

A、1 B、2 C、3 D、4
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:解答题
已知二次函数的图象的顶点坐标为(3,-2)且与 轴交与(0,
轴交与(0, )
)
(1)求函数的解析式
(2)当 为何值时,
为何值时, 随
随 增大而增大? 当
增大而增大? 当 为何值时,函数值是非负数?
为何值时,函数值是非负数?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:填空题
将抛物线 的图象向右平移1个单位,再向上平移2个单位后,得到的新抛物线解析式是 .
的图象向右平移1个单位,再向上平移2个单位后,得到的新抛物线解析式是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省丽水市莲都区九年级第一次中考模拟数学试卷(解析版) 题型:解答题
(本题8分)为提高初中生的身体素质,教育行政部门规定:初中生每天参加户外活动的平均时间应不少于1小时.为了解学生参加户外活动的情况,某县教育行政部门对部分学生参加户外活动的时间进行了抽样调查,并将调查结果绘制成下列两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)这次抽样共调查了 名学生,并补全条形统计图;
(2)计算扇形统计图中表示户外活动时间0.5小时的扇形圆心角度数;
(3)本次调查学生参加户外活动的平均时间是否符合要求?(写出判断过程)


查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级直升班第一次综合测试数学试卷(解析版) 题型:选择题
如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA、OB在0点钉在一起,并使它们保持垂直,在测直径时,把0点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )

A.12个单位 B.10个单位 C.4个单位 D.15个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com