Question

【题目】如图，在Rt△ABC中，∠C=90°，点D是AC的中点，且∠A+∠CDB=90°，过点A，D作⊙O，使圆心O在AB上，⊙O与AB交于点E．

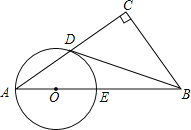
（1）求证：直线BD与⊙O相切；

（2）若AD：AE=，BC=6，求切线BD的长．

Answer 1

【答案】（1）见解析；（2）3．

【解析】

试题分析：（1）如图，连接OD，欲证明直线BD与⊙O相切，只需证明OD⊥BD即可；

（2）连接DE．利用圆周角定理和三角形中位线定理易求DE的长度，而AD：AE=，在直角△ADE中，利用勾股定理即可求得AE的长度；最后利用切割线定理来求切线BD的长度．

（1）证明：∵OA=OD，

∴∠A=∠ADO（等边对等角）．

又∵∠A+∠CDB=90°（已知），

∴∠ADO+∠CDB=90°（等量代换），

∴∠ODB=180°﹣（∠ADO+∠CDB）=90°，即BD⊥OD．

又∵OD是圆O的半径．

∴BD是⊙O切线；

（2）解：连接DE，则∠ADE=90°（圆周角定理）．

∵∠C=90°，

∴∠ADE=∠C，

∴DE∥BC，

又∵D是AC中点，

∴DE是△ABC的中位线，

∴DE=BC=3，AE=BE．

∵AD：AE=，

在直角△ADE中，利用勾股定理求得AE=3，则AB=6．

∴BD2=ABBE=6×3=54，

∴BD=3．