
(本题9分)如图,对称轴为x=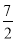 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
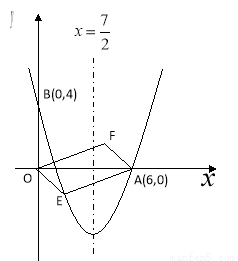
(1)求抛物线解析式;
(2)设点E(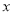 ,
,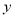 )是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与
)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与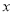 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量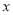 的取值范围;
的取值范围;
①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
(1)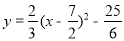 (2)见解析
(2)见解析
【解析】
试题分析:(1)理由待定系数法进行求解,将解析式设为顶点式,然后计算;(2)根据四边形的面积求出点E的坐标,然后分别进行判断;(3)根据正方形的性质求出点E的坐标,然后进行说明.
试题解析:(1)设抛物线的解析式为y=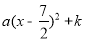 .
.
把A、B两点坐标代入上式,得 解得
解得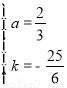 .
.
所以抛物线的解析式为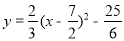 .
.
(2)因为点E(x,y)在抛物线上,位于第四象限,且坐标适合抛物线的解析式,
所以y<0,即-y>0,-y表示点E到OA的距离.
因为OA是平行四边形OEAF的对角线,所以S=2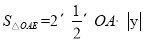 =-6y=-4
=-6y=-4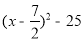
因为抛物线与x轴的两个交点是(1,0)和(6,0),所以,自变量x的取值范围是1<x<6.
①依题意,当S=24时,即-4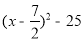 =24,解得
=24,解得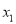 =3,
=3,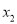 =4.
=4.
所以点E的坐标为(3,-4)或(4,-4).
E(3,-4)满足OE=AE,所以四边形OEAF是菱形;
E(4,-4)不满足OE=AE,所以四边形OEAF不是菱形.
②当OA⊥EF,且OA=EF时,四边形OEAF是正方形,此时点E的坐标只能是(3,-3),而点(3,-3)不在抛物线上,故不存在这样的点E,使四边形OEAF是正方形.
考点:待定系数法求二次函数的解析式、菱形与正方形的性质.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源:2014-2015学年山东省潍坊地区九年级上学期期末质量评估数学试卷(解析版) 题型:解答题
(本题满分12分)AB是⊙O的直径,AD与⊙O相交,点C是⊙O上一点,经过点C的直线交AD于点E.
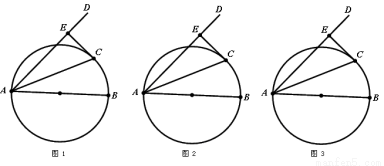
(1)如图1 ,若AC平分∠BAD,CE⊥AD于点E,求证:CE是⊙O的切线;
(2)如图2,若CE是⊙O的切线,CE⊥AD于点E,AC是∠BAD的平分线吗?说明理由;
(3)如图3,若CE是⊙O的切线,AC平分∠BAD,AB=8,AC=6,求AE的长度.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省南阳市九年级上期期末摸底数学试卷(解析版) 题型:选择题
如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若cos∠BDC=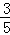 ,则BC的长是( )
,则BC的长是( )
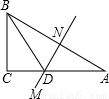
A.4cm B.6cm C.8cm D.10cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年甘肃省白银市会宁县九年级上学期期末考试数学试卷(解析版) 题型:填空题
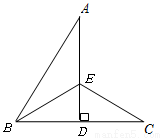
如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连结EC,则∠AEC的度数是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年甘肃省白银市会宁县九年级上学期期末考试数学试卷(解析版) 题型:选择题
某农场的粮食总产量为1500吨,设该农场人数为 人,平均每人占有粮食数为
人,平均每人占有粮食数为 吨,则
吨,则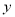 与
与 之间的函数图象大致是( )
之间的函数图象大致是( )

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市九年级上学期期末考试数学试卷(解析版) 题型:解答题
(6分)如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且AB = 26m,OE⊥CD于点E.水位正常时测得OE∶CD=5∶24
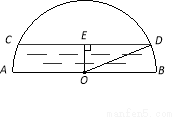
(1)求CD的长;
(2)现汛期来临,水面要以每小时4 m的速度上升,则经过多长时间桥洞会刚刚被灌满?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市九年级上学期期末考试数学试卷(解析版) 题型:填空题
在一个不透明的盒子中装有2个白球,n个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为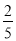 ,则n=___________。
,则n=___________。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古包头市九年级上学期期末考试数学试卷(解析版) 题型:填空题
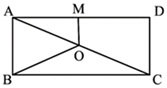
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省郴州市八年级上学期期中考试数学试卷(解析版) 题型:选择题
下列计算正确的是( )
A、2?2= ?4 B、2?2= 4 C、2?2=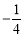 D、2?2=
D、2?2=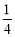
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com