
(本题满分12分)AB是⊙O的直径,AD与⊙O相交,点C是⊙O上一点,经过点C的直线交AD于点E.
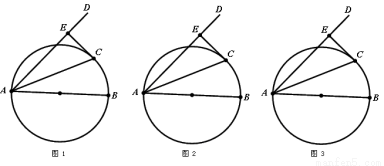
(1)如图1 ,若AC平分∠BAD,CE⊥AD于点E,求证:CE是⊙O的切线;
(2)如图2,若CE是⊙O的切线,CE⊥AD于点E,AC是∠BAD的平分线吗?说明理由;
(3)如图3,若CE是⊙O的切线,AC平分∠BAD,AB=8,AC=6,求AE的长度.
(1)(2)见解析 (3)AE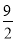
【解析】
试题分析:(1)首先连接OC,根据OA=OC得出∠OAC=∠OCA,根据角平分线的性质得出∠OCA=∠CAD,得到OC∥AE,从而说明CE为切线;(2)方法同(1);(3)根据切线的性质来证明△ABC和△ACE相似,从而求出AE的长度.
试题解析:(1)证明:连接OC ∵OA=OC ∴∠OAC=∠OCA ∵AC平分∠BAD ∴∠OCA=∠CAD
∴OC∥AD ∵CE⊥AD ∴CE⊥OC 又∵OC是半径 ∴CE是⊙O的切线。
(2)【解析】
AC是∠BAD的平分线
理由:连接OC ∵CE是⊙O的切线 ∴CE⊥OC ∵CE⊥AD ∴OC∥AD
∴∠OCA=∠CAD ∵OA=OC ∴∠OAC=∠OCA ∴∠OCA=∠CAD 即:AC是∠BAD的平分线
(3)【解析】
连接OC、BC ∵CE是⊙0的切线 ∴CE⊥OC ∵AB是⊙O的直径 ∴∠ACB=900
∴∠ACE=∠OCB ∵OB=OC ∴∠B=∠OCB ∴∠B=∠ACE
∵AC平分∠BAD ∴△ABC∽△ACE
∴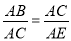 即:
即: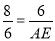 解得:AE=
解得:AE=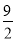
考点:切线的判定与性质、三角形相似的判定与性质.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县八年级上学期期中调研数学试卷(解析版) 题型:选择题
下列结论正确的是
A.有两个锐角相等的两个直角三角形全等
B.一条斜边对应相等的两个直角三角形全等
C.两个等边三角形全等
D.顶角和底边对应相等的两个等腰三角形全等
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市青春共同体九年级上学期期中考试数学试卷(解析版) 题型:填空题
△ABC中,∠A、∠B都是锐角,若sinA=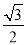 ,cosB=
,cosB=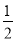 ,则∠C= .
,则∠C= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市青春共同体九年级上学期期中考试数学试卷(解析版) 题型:选择题
把一个小球以20米/秒的速度竖起向上弹出,它在空中的高度h(米)与时间t(秒),满足关系h=20t-5t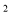 ,当小球达到最高点时,小球的运动时间为( )
,当小球达到最高点时,小球的运动时间为( )
A.1秒 B. 2秒 C.4秒 D.20秒
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省潍坊地区九年级上学期期末质量评估数学试卷(解析版) 题型:解答题
(本题满分10分)市某楼盘准备以每平方米6 000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4 860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省潍坊地区九年级上学期期末质量评估数学试卷(解析版) 题型:选择题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
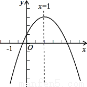
①abc<0;②b>a+c;③2a-b=0;④b2-4ac<0.其中正确的结论个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省南阳市九年级上期期末摸底数学试卷(解析版) 题型:解答题
(9分)某工厂生产的某种产品按质量分为10个档次,第一档次(最低档次)的产品一天可生产80件,每件产品的利润为10元,每提高一个档次,每件产品的利润增加2元.
(1)当每件产品的利润为16元时,此产品质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天的产量减少4件.若生产某档次产品一天的总利润为1200元,问该工厂生产的是第几档次的产品?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题9分)如图,对称轴为x=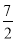 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
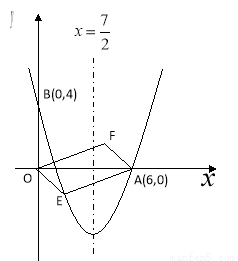
(1)求抛物线解析式;
(2)设点E(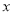 ,
,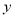 )是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与
)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与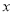 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量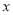 的取值范围;
的取值范围;
①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com