
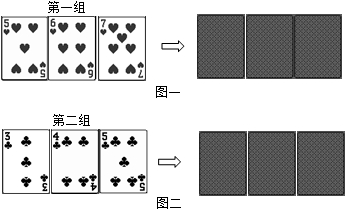
分析 (1)由第一组分别是红桃5、红桃6、红桃7,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图或列出表格,然后由树状图或表格求得所有等可能的结果与抽出一对牌(即数字相同)”的情况,再利用概率公式即可求得答案.
解答 解:(1)第一组分别是红桃5、红桃6、红桃7,
∴P(抽到红桃6)=$\frac{1}{3}$;
(2)方法一:画树状图如下: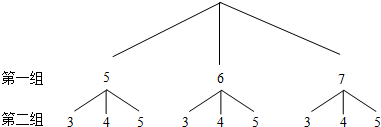
∵由树状图可知,共有9种机会均等的情况,其中抽出一对牌(即数字相同)只有一种情况,
∴P(抽出一对牌)=$\frac{1}{9}$.
方法二:列表如下:
| 3 | 4 | 5 | |
| 5 | (5,3) | (5,4) | (5,5) |
| 6 | (6,3) | (6,4) | (6,5) |
| 7 | (7,3) | (7,4) | (7,5) |
点评 此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:填空题
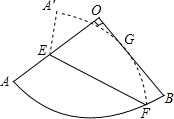 如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A′F}$恰好与半径OB相切于点G,若OE=5,则O到折痕EF的距离为$\sqrt{15}$.
如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A′F}$恰好与半径OB相切于点G,若OE=5,则O到折痕EF的距离为$\sqrt{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 每天出次品的个数 | 0 | 2 | 3 | 4 |
| 天数 | 3 | 2 | 4 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com