
已知,如图,在Rt△ABC中,∠ABC=90°∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB、AC交于点G、F.
(1)求证:GE=GF
(2)若BD=1,求DF的长。

(1)证明见解析;(2) .
.
【解析】
试题分析:(1)根据已知条件易证明Rt△AEC≌Rt△DFC,得CE=CF,则DE=AF,从而进一步证明Rt△AFG≌Rt△DEG,就可得到GE=GF;
(2)根据直角三角形的性质可以得到CE=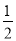 AC,则CE=
AC,则CE=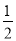 CD,即AB是CE的垂直平分线,则BC=BD=1.再根据直角三角形的性质进一步求得AB、BE的长,则AE=AB-BE,结合(1)中的全等三角形,知DF=AE.
CD,即AB是CE的垂直平分线,则BC=BD=1.再根据直角三角形的性质进一步求得AB、BE的长,则AE=AB-BE,结合(1)中的全等三角形,知DF=AE.
(1)证明:∵DF∥BC,∠ACB=90°,
∴∠CFD=90°.
∵CD⊥AB,
∴∠AEC=90°.
在Rt△AEC和Rt△DFC中,∠AEC=∠CFD=90°,∠ACE=∠DCF,DC=AC,
∴Rt△AEC≌Rt△DFC.
∴CE=CF.
∴DE=AF.
而∠AGF=∠DGE,∠AFG=∠DEG=90°,
∴Rt△AFG≌Rt△DEG.
∴GF=GE.
(2)【解析】
∵CD⊥AB,∠A=30°,
∴CE=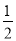 AC=
AC=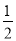 CD.
CD.
∴CE=ED.
∴BC=BD=1.
又∵∠ECB+∠ACE=90°,∠A+∠ACE=90°,
∴∠ECB=∠A=30°,∠CEB=90°,
∴BE=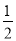 BC=
BC=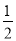 BD=
BD=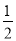 .
.
在直角三角形ABC中,∠A=30°,
则AB=2BC=2.
则AE=AB-BE= .
.
∵Rt△AEC≌Rt△DFC,
∴DF=AE= .
.
考点:1.勾股定理;2.直角三角形全等的判定.


科目:初中数学 来源:2013-2014学年安徽省淮北市九年级下学期五校联考五数学试卷(解析版) 题型:解答题
在图1至图4中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE和AD在同一直线上.
操作示例:
当AE<a时,如图1,在BA上选取适当的点G,BG=b,连接FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置,恰能构成四边形FGCH.
思考发现:小明在操作后发现:该剪拼方法是先将△FAG绕点F逆时针旋转90°到△FEH的位置,易知EH与AD在同一直线上,连接CH.由剪拼方法可得DH=BG,从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图所示),
实践探究:
(1)小明判断出四边形FGCH是正方形,请你给出判断四边形FGCH是正方形的方法。
(2)经测量,小明发现图1中BG是AE一半,请你证明小明的发现是正确的。(提示:过点F作FM⊥AH,垂足为点M);
拓展延伸
类比图1的剪拼方法,请你就图2至图4的三种情形分别画出剪拼成一个新正方形的示意图

查看答案和解析>>
科目:初中数学 来源:2013-2014学年安徽省当涂县四校九年级上学期期末联考数学试卷(解析版) 题型:选择题
已知点(-1,y1)、(2,y2)、(3,y3)在反比例函数 的图象上.下列结论中正确的是
的图象上.下列结论中正确的是
A.y1>y2>y3 B.y1>y3>y2 C.y3>y1>y2 D.y2>y3>y1
查看答案和解析>>
科目:初中数学 来源:2013-2014学年安徽十大名校九年级第四次月考数学试卷(解析版) 题型:选择题
如图表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,那么该几何体的主视图为
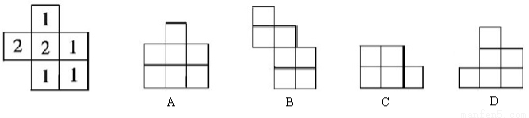
查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省乐山市夹江县九年级毕业会考适应性考试数学试卷(解析版) 题型:解答题
如图,已知反比例函数 (
( )与一次函数
)与一次函数 (
( )相交于A、B两点,AC⊥
)相交于A、B两点,AC⊥ 轴于点C.若△OAC的面积为1,且tan∠AOC=2.
轴于点C.若△OAC的面积为1,且tan∠AOC=2.
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当 为何值时,反比例函数
为何值时,反比例函数 的值大于一次函数
的值大于一次函数 的值?
的值?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年吉林省长春市朝阳区中考一模数学试卷(解析版) 题型:选择题
如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=35°,则∠2的度数为( )

A.35° B.65° C.85° D.95°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com