
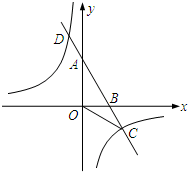
 如图,已知A、B两点的坐标分别为A(0,2
如图,已知A、B两点的坐标分别为A(0,2| 3 |
| m |
| x |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| m |
| x |
3
| ||
| x |
|
| 3 |
| 1 |
| 2 |
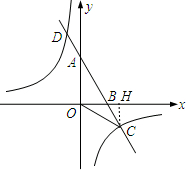 解:(1)设直线AB的解析式为y=kx+b,
解:(1)设直线AB的解析式为y=kx+b,| 3 |
|
|
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| m |
| x |
| 3 |
| 3 |
3
| ||
| x |
|
|
|
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 小明和同学去公园游玩,他们在一个平台上看见一个移动通信的信号转播铁塔,他们决定尝试着测量这个铁塔的高度,于是,小明来到平台的边缘的C处,测得仰角为45°,他们沿着台阶往下走,来到第二个平台的E处,测得仰角为30°,(其中,点A、C、D、E在同一平面上)小明和同学发现台阶共10级,每阶高20厘米,每阶宽30厘米,另测得E点到台阶的边缘D处距离为8米,请你利用上述数据求出铁塔AB的高度.(
小明和同学去公园游玩,他们在一个平台上看见一个移动通信的信号转播铁塔,他们决定尝试着测量这个铁塔的高度,于是,小明来到平台的边缘的C处,测得仰角为45°,他们沿着台阶往下走,来到第二个平台的E处,测得仰角为30°,(其中,点A、C、D、E在同一平面上)小明和同学发现台阶共10级,每阶高20厘米,每阶宽30厘米,另测得E点到台阶的边缘D处距离为8米,请你利用上述数据求出铁塔AB的高度.(| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
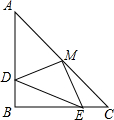 如图,在△ABC中,AB=AC,∠B=90°,D、E分别为AB、BC上的动点,且BD=CE,M是AC的中点,试探究在DE运动的过程中,△DEM的形状是否发生变化?它是什么形状的三角形?
如图,在△ABC中,AB=AC,∠B=90°,D、E分别为AB、BC上的动点,且BD=CE,M是AC的中点,试探究在DE运动的过程中,△DEM的形状是否发生变化?它是什么形状的三角形?查看答案和解析>>
科目:初中数学 来源: 题型:
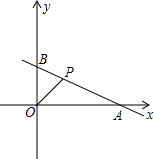 在直角坐标系中,已知点A(4,0),B(0,2),点P(x,y)在第一象限内,且x+2y=4,设△AOP的面积是S.
在直角坐标系中,已知点A(4,0),B(0,2),点P(x,y)在第一象限内,且x+2y=4,设△AOP的面积是S. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com