
 如图,这是函数( )的大致图象.
如图,这是函数( )的大致图象.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
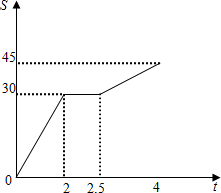 如图、这是小明骑自行车外出旅游时间的路程S(千米)与时间t(小时)间的函数关系图,观察图中提供的数据,解答下列问题.
如图、这是小明骑自行车外出旅游时间的路程S(千米)与时间t(小时)间的函数关系图,观察图中提供的数据,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com