
如图,已知抛物线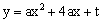 (a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0).
(a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0).
(1)求此抛物线的对称轴及点A的坐标;
(2)过点C作x轴的平行线交抛物线的对称轴于点P,你能
判断四边形ABCP是什么四边形吗?请证明你的结论;
(3)连结AC,BP,若AC⊥BP,试求此抛物线的解析式.
 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
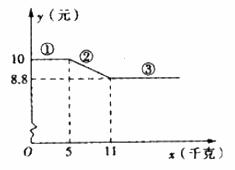
在某水果店一次性购买A种水果的单价y(元)与购买量x(千克)的函数关系如图所示。
(1)下列关于三段函数图象的说法不正确的是( )
A. 第①段函数图象表示数量不多于5千克时,单价为10元。
B. 第③段函数图象表示数量不少于11千克时,单价为8.8元。
C. 第②段函数图象可知:当一次性数量多于5千克但不多于11千克时,每多买1千克,单价就降低1.2元。
(2)求图中第②段函数图象的解析式,并指出x的取值范围。
(3)某天老李计划用90元去该店买A种水果,问老李一次性(或最多)能买回多少千克A种水果?
查看答案和解析>>
科目:初中数学 来源: 题型:
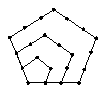
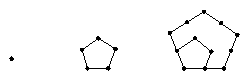
用棋子按下列方式摆图形,第一个图形有1枚棋子,第二个图形有5枚棋子,第三个图形有12枚棋子,…
依此规律,第7个图形比第6个图形多( )枚棋子
| |||||
 | |||||
 | |||||
|
|
|
|
A.20 B.19 C.18 D.17
查看答案和解析>>
科目:初中数学 来源: 题型:
如图①,在□ABCD中,对角线AC⊥AB,BC=10,tan∠B=2.点E是BC边上的动点,过点E作
EF⊥BC于点E,交折线AB-AD于点F,以EF为边在其右侧作正方形EFGH,使EH边落在射线BC上.点E从点B出发,以每秒1个单位的速度在BC边上运动,当点E与点C重合时,点E停止运动,设点E的运动时间为t(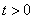 )秒.
)秒.
(1)□ABCD的面积为 ;当t= 秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG, 得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com