
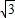 矩形,如图(3),连接EF,GH,IJ,KL.若图中阴影部分四个三角形的面积和为12
矩形,如图(3),连接EF,GH,IJ,KL.若图中阴影部分四个三角形的面积和为12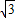 ,求?ABCD的面积?
,求?ABCD的面积?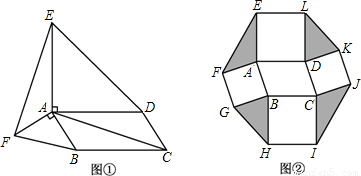
 AF×EQ=3,同理S△CIJ=3,SLDK=
AF×EQ=3,同理S△CIJ=3,SLDK= LD×KW=
LD×KW= AD×BO=
AD×BO= ×6=3,即可得出答案;
×6=3,即可得出答案;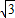 a,AB=CD=
a,AB=CD=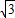 b,∠BAD=∠BCD,求出∠EAQ=∠BAD=∠BCS,∠Q=∠BSC=90°,证△EQA∽△BSC,求出BS=
b,∠BAD=∠BCD,求出∠EAQ=∠BAD=∠BCS,∠Q=∠BSC=90°,证△EQA∽△BSC,求出BS=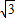 EQ,求出S平行四边形ABCD=6S△EAF,同理S平行四边形ABCD=6S△LDK=6S△GBH=6S△ICJ,求出S△EAF=S△LDK=S△GBH=S△ICJ=3
EQ,求出S平行四边形ABCD=6S△EAF,同理S平行四边形ABCD=6S△LDK=6S△GBH=6S△ICJ,求出S△EAF=S△LDK=S△GBH=S△ICJ=3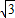 ,即可得出答案.
,即可得出答案. 在△FAE和△ABC中
在△FAE和△ABC中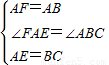 ,
,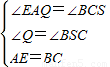 ,
, AF×EQ=
AF×EQ= ×6=3,
×6=3, LD×KW=
LD×KW= AD×BO=
AD×BO= ×6=3,
×6=3,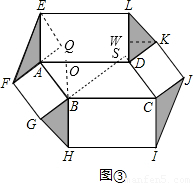
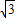 a,AB=CD=
a,AB=CD=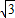 b,∠BAD=∠BCD,
b,∠BAD=∠BCD, =
=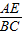 =
=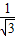 ,
,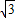 EQ,
EQ, a,AF=b,
a,AF=b, AF×EQ=
AF×EQ= b•EQ,
b•EQ,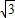 b•
b• EQ=3×2×
EQ=3×2× b•EQ=6S△EAF,
b•EQ=6S△EAF,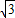 ,
,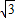 ,
,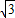 =18
=18 .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
| 3 |
| 3 |


查看答案和解析>>
科目:初中数学 来源:2013年浙江省金华市六校联谊中考模拟数学试卷(带解析) 题型:解答题
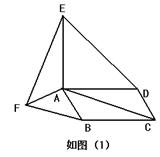
探究:如图(1),在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=900,连接AC,EF。在图中找一个与△FAE全等的三角形,并加以证明。
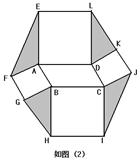
应用:以□ABCD的四条边为边,在其形外分别作正方形,如图(2),连接EF,GH,IJ,KL。若□ABCD的面积为6,则图中阴影部分四个三角形的面积和为____________.
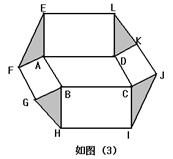
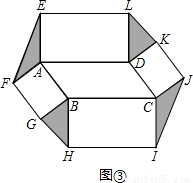
推广:以□ABCD的四条边为矩形长边,在其形外分别作长与宽之比为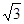 矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12
矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12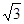 ,求□ABCD的面积?
,求□ABCD的面积?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市昌平区九年级第一学期期末考试数学试卷(解析版) 题型:解答题
阅读下面的材料:
小明遇到一个问题:如图(1),在□ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G. 如果 ,求
,求 的值.
的值.

他的做法是:过点E作EH∥AB交BG于点H,则可以得到△BAF∽△HEF.
请你回答:(1)AB和EH的数量关系为 ,CG和EH的数量关系为 , 的值为 .
的值为 .
(2)如图(2),在原题的其他条件不变的情况下,如果 ,那么
,那么 的值为 (用含a的代数式表示).
的值为 (用含a的代数式表示).

(3)请你参考小明的方法继续探究:如图(3),在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F. 如果 ,那么
,那么 的值为 (用含m,n的代数式表示).
的值为 (用含m,n的代数式表示).

查看答案和解析>>
科目:初中数学 来源:2013年浙江省金华市六校联谊中考模拟数学试卷(解析版) 题型:解答题
探究:如图(1),在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=900,连接AC,EF。在图中找一个与△FAE全等的三角形,并加以证明。
应用:以□ABCD的四条边为边,在其形外分别作正方形,如图(2),连接EF,GH,IJ,KL。若□ABCD的面积为6,则图中阴影部分四个三角形的面积和为____________.

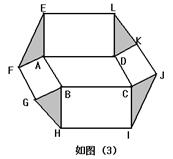
推广:以□ABCD的四条边为矩形长边,在其形外分别作长与宽之比为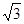 矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12
矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12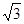 ,求□ABCD的面积?
,求□ABCD的面积?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com