
 时,直接写出∠DEF的度数;
时,直接写出∠DEF的度数; ,∠DEF=
,∠DEF= (
( <X<
<X< ,
, <Y<
<Y< ),求:Y关于X的函数解析式及相应自变量X的取值范围,
),求:Y关于X的函数解析式及相应自变量X的取值范围, 
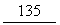 °;…………2分
°;…………2分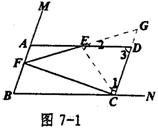
 时,点F在线段AB上(见图7-1)。
时,点F在线段AB上(见图7-1)。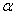 。
。 ABCD,∴ AB∥CD,AD=BC,AB=CD,∠3=∠B=x°。
ABCD,∴ AB∥CD,AD=BC,AB=CD,∠3=∠B=x°。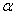 。
。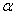 。
。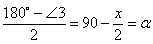 。
。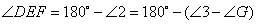
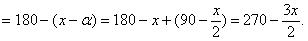 …………3分
…………3分 ,
, 仍成立。…………4分
仍成立。…………4分
 时,点F在线段AB的延长线上(见图7-4)。
时,点F在线段AB的延长线上(见图7-4)。 。…………6分
。…………6分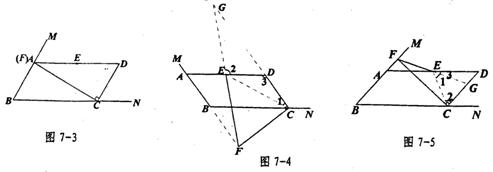
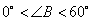 时,点F在线段BA的延长线上(如图7-5)。
时,点F在线段BA的延长线上(如图7-5)。 ,
, 。…………7分
。…………7分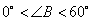 时,
时,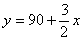 ;
; 时,
时, 。
。 时,四边形ABCD是矩形,F点和B点重合,从而得出∠DEF的度数;
时,四边形ABCD是矩形,F点和B点重合,从而得出∠DEF的度数;

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源:不详 题型:解答题
 与x轴、y轴分别相交于点A和点B,直线
与x轴、y轴分别相交于点A和点B,直线 经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.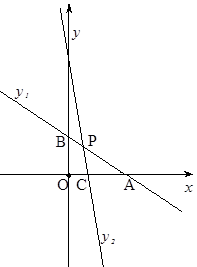
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与
与 成正比例,且
成正比例,且 时,
时,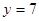 .
.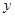 与
与 的函数关系式;
的函数关系式;  时,求
时,求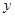 的值;
的值;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ≤3,且
≤3,且 取整数).而从4月份起,棉价大幅度走低,其价格y2(元/吨)与月份
取整数).而从4月份起,棉价大幅度走低,其价格y2(元/吨)与月份 (4≤x≤6,且x取整数)之间的函数关系如图所示.
(4≤x≤6,且x取整数)之间的函数关系如图所示. 之间所满足的一次函数关系式;
之间所满足的一次函数关系式; 取整数);4至6月份棉花进货量p2(吨)与月份
取整数);4至6月份棉花进货量p2(吨)与月份 之间所满足的函数关系式为p2=40x-20 (4≤
之间所满足的函数关系式为p2=40x-20 (4≤ ≤6,且
≤6,且 取整数).求在前6个月中该棉被厂的棉花进货金额最大的月份和该月的进货金额;
取整数).求在前6个月中该棉被厂的棉花进货金额最大的月份和该月的进货金额; %.若要使7月份进货金额为5130400元,请你估算出
%.若要使7月份进货金额为5130400元,请你估算出 的最大整数值.
的最大整数值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com