
【题目】某电器超市销售A、B两种不同型号的电风扇,每种型号电风扇的购买单价分别为每台310元,460元.
(1)若某单位购买A,B两种型号的电风扇共50台,且恰好支出20000元,求A,B两种型号电风扇各购买多少台?
(2)若购买A,B两种型号的电风扇共50台,且支出不超过18000元,求A种型号电风扇至少要购买多少台?
【答案】(1)购买A种型号电风扇20台,B型种型号电风扇30台;
(2)A种型号电风扇至少要购买34台
【解析】试题分析:(1)设购买A种型号电风扇x套,B型号的电风扇y套,根据:“A,B两种型号的电风扇共50套、共支出20000元”列方程组求解可得;
(2)设购买A型号电风扇m套,根据:A型电风扇总费用+B型电风扇总费用≤18000,列不等式求解可得.
试题解析:
(1)设购买A种型号电风扇x台,B种型号电风扇y台,
根据题意,得: ![]() , 解得:x=20,y=30,
, 解得:x=20,y=30,
答:购买A种型号电风扇20台,B型种型号电风扇30台.
(2)设购买A种型号电风扇m台,
根据题意,得:310m+460(50-m)≤18000,
解得:m≥33![]() ,
,
∵m为整数,∴m的最小值为34,
答:A种型号电风扇至少要购买34台.


科目:初中数学 来源: 题型:
【题目】下列各式与2x-(-3y-4z)相等的是( )
A. 2x+(-3y+4z) B. 2x+(3y+4z)
C. 2x+(3y-4z) D. 2x+(-3y-4z)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求解:如图,在△ABC中,∠A=42°,∠ABC和∠ACB的平分线相交于点D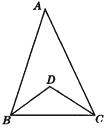
(1)求∠BDC的度数.
(2)在(1)中去掉∠A=42°这个条件,请探究∠BDC和∠A之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,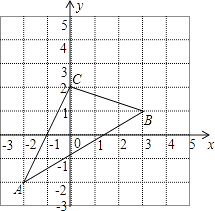
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 近似数25.0的精确度与近似数25的精确度一样
B. 近似数5千克的精确度和近似数5000克的精确度一样
C. 近似数1.4×104的精确度与近似数14千的精确度一样
D. 今天的温度是28 ℃,那么28 ℃是准确数
查看答案和解析>>
科目:初中数学 来源: 题型:
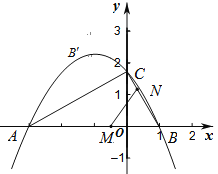
【题目】如图,已知点![]() ,二次函数
,二次函数![]() 的对称轴为直线
的对称轴为直线![]() ,其图象过点
,其图象过点![]() 与
与![]() 轴交于另一点
轴交于另一点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求二次函数的解析式,写出顶点坐标;
(2)动点![]() 同时从
同时从![]() 点出发,均以每秒2个单位长度的速度分别沿
点出发,均以每秒2个单位长度的速度分别沿![]() 的
的![]() 边上运动,设其运动的时间为
边上运动,设其运动的时间为![]() 秒,当其中一个点到达终点时,另一个点也随之停止运动.连结
秒,当其中一个点到达终点时,另一个点也随之停止运动.连结![]() ,将
,将![]() 沿
沿![]() 翻折,若点
翻折,若点![]() 恰好落在抛物线弧上的
恰好落在抛物线弧上的![]() 处,试求
处,试求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(3)在(2)的条件下,Q为BN的中点,试探究坐标轴上是否存在点![]() ,使得以
,使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?如果存在,请求出点
相似?如果存在,请求出点![]() 的坐标;如果不存在,试说明理由.
的坐标;如果不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容. 证明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (),
∴∠2﹢﹦180°.
∴EH∥AB ().
∴∠B﹦∠EHC().
∵∠3﹦∠B(已知)
∴∠3﹦∠EHC().
∴DE∥BC().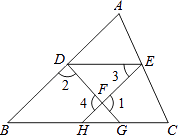
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点Q为坐标系上任意一点,某图形上的所有点在∠Q的内部(含角的边),这时我们把∠Q的最小角叫做该图形的视角.如图1,矩形ABCD,作射线OA,OB,则称∠AOB为矩形ABCD的视角.
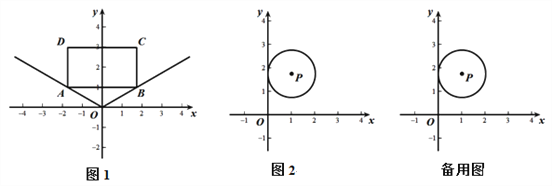
(1)如图1,矩形ABCD,A(﹣![]() ,1),B(
,1),B(![]() ,1),C(
,1),C(![]() ,3),D(﹣
,3),D(﹣![]() ,3),直接写出视角∠AOB的度数;
,3),直接写出视角∠AOB的度数;
(2)在(1)的条件下,在射线CB上有一点Q,使得矩形ABCD的视角∠AQB=60°,求点Q的坐标;
(3)如图2,⊙P的半径为1,点P(1, ![]() ),点Q在x轴上,且⊙P的视角∠EQF的度数大于60°,若Q(a,0),求a的取值范围.
),点Q在x轴上,且⊙P的视角∠EQF的度数大于60°,若Q(a,0),求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com