
����Ŀ����ƽ��ֱ������ϵ�У���QΪ����ϵ������һ�㣬ijͼ���ϵ����е��ڡ�Q���ڲ������ǵıߣ�����ʱ���ǰѡ�Q����С�ǽ�����ͼ�ε��ӽǣ���ͼ1������ABCD��������OA��OB����ơ�AOBΪ����ABCD���ӽǣ�
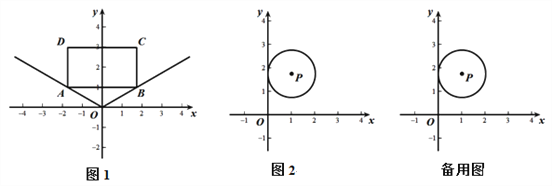
��1����ͼ1������ABCD��A����![]() ��1����B��
��1����B��![]() ��1����C��
��1����C��![]() ��3����D����
��3����D����![]() ��3����ֱ��д���ӽǡ�AOB�Ķ�����
��3����ֱ��д���ӽǡ�AOB�Ķ�����
��2���ڣ�1���������£�������CB����һ��Q��ʹ�þ���ABCD���ӽǡ�AQB=60�������Q�����ꣻ
��3����ͼ2����P�İ뾶Ϊ1����P��1�� ![]() ������Q��x���ϣ��ҡ�P���ӽǡ�EQF�Ķ�������60������Q��a��0������a��ȡֵ��Χ��
������Q��x���ϣ��ҡ�P���ӽǡ�EQF�Ķ�������60������Q��a��0������a��ȡֵ��Χ��
���𰸡���1���ӽǡ�AOB�Ķ�����120�㣻
��2��Q�����꣨![]() ����1����
����1����
��3��a��ȡֵ��Χ��0��a��2��
�������������������1����A����![]() ��1����B��
��1����B��![]() ��1������OA��OB��y��ļнǶ�Ϊ60�㣬���Ը����ӽǵĶ���ij��ӽ���AOB�Ķ�����120������2������AC��������CB�Ͻ�ȡCQ=CA������AQ�����ɹ�����ȱ������Σ��ó��ӽ�Ϊ60���ʱ��Q�����꼴�ɣ���3������Q���O�غ�ʱ��aȡ��Сֵ����FQ��x��ʱ��aȡ���ֵ.
��1������OA��OB��y��ļнǶ�Ϊ60�㣬���Ը����ӽǵĶ���ij��ӽ���AOB�Ķ�����120������2������AC��������CB�Ͻ�ȡCQ=CA������AQ�����ɹ�����ȱ������Σ��ó��ӽ�Ϊ60���ʱ��Q�����꼴�ɣ���3������Q���O�غ�ʱ��aȡ��Сֵ����FQ��x��ʱ��aȡ���ֵ.
����������⣺��1��120����
��2������AC��������CB�Ͻ�ȡCQ=CA������AQ��
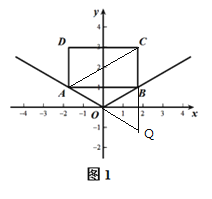
��AB=2![]() ��BC=2��
��BC=2��
��AC=4��
���ACQ=60����
���ACQΪ�ȱ������Σ�
����AQC=60����
��CQ=AC=4��
��Q��![]() ����1����
����1����
��3����ͼ2������Q���O�غ�ʱ����EQF=60����
��Q��0��0����
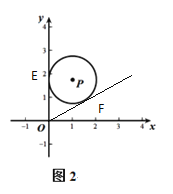
��ͼ3����FQ��x��ʱ����EQF=60����
��Q��2��0����

��a��ȡֵ��Χ��0��a��2��


 ȫ��������ϵ�д�
ȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������A��B���ֲ�ͬ�ͺŵĵ���ȣ�ÿ���ͺŵ���ȵĹ��۷ֱ�Ϊÿ̨310Ԫ��460Ԫ��
��1����ij��λ����A��B�����ͺŵĵ���ȹ�50̨����ǡ��֧��20000Ԫ����A��B�����ͺŵ���ȸ��������̨��
��2��������A��B�����ͺŵĵ���ȹ�50̨����֧��������18000Ԫ����A���ͺŵ��������Ҫ�������̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ȫ���˽�ѧ����ѧϰ�������ͥ�Ļ����������ǿѧУ����ͥ����ϵ��÷����ѧ������֯ȫ���ʦ��չ���������һ��������ʦ�����ڰ༶��ȫ��ѧ������ʵ�ؼҷã��˽ÿ��ѧ����ͥ�������Ϣ���ȴ��������ȡ15��ѧ����ͥ����������������������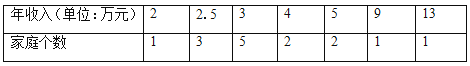
��1������15��ѧ����ͥ�������ƽ��������λ����������
��2������Ϊ�ã�1���е��ĸ�������������15��ѧ����ͥ�������һ��ˮƽ��Ϊ���ʣ����Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��![]() ��x�ᣬy��ֱ���A��B���㣬��A����ֱ��
��x�ᣬy��ֱ���A��B���㣬��A����ֱ��![]() �ĶԳƵ�Ϊ��C��
�ĶԳƵ�Ϊ��C��
��1�����C�����ꣻ
��2����������![]() ����A��B��C���㣬��������ߵı���ʽ��
����A��B��C���㣬��������ߵı���ʽ��
��3����������![]() ����A��B���㣬�Ҷ����ڵڶ����ޣ����������߶�AC�����������㣬��a��ȡֵ��Χ��
����A��B���㣬�Ҷ����ڵڶ����ޣ����������߶�AC�����������㣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PΪ����������y= ![]() ��ͼ����һ�㣬PA��x���ڵ�A����PAO�����Ϊ6�������и�����Ҳ���������������ͼ���ϵ��ǣ� ��
��ͼ����һ�㣬PA��x���ڵ�A����PAO�����Ϊ6�������и�����Ҳ���������������ͼ���ϵ��ǣ� �� 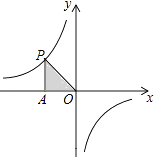
A.��2��3��
B.����2��6��
C.�� 2��6 ��
D.����2��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��Q�Ƿ���������y= ![]() ͼ���ϵ����㣬PA��y���ڵ�A��QN��x���ڵ�N����PM��x���ڵ�M��QB��y���ڵ�B������PB��QM����ABP�������ΪS1 �� ��QMN�������ΪS2 �� ��S1S2 �� �������������=����
ͼ���ϵ����㣬PA��y���ڵ�A��QN��x���ڵ�N����PM��x���ڵ�M��QB��y���ڵ�B������PB��QM����ABP�������ΪS1 �� ��QMN�������ΪS2 �� ��S1S2 �� �������������=���� 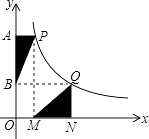
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD��ֱ��MN�ֱ�AB��CD�ڵ�E��F��EGƽ�֡�AEF��EG��FG�ڵ�G������BEM=60�㣬���CFG= �� 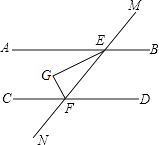
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻ�����ڵ�һ����x�ᡢy�����������ڵ�һ���ӣ�����ԭ����������0��1����Ȼ����Ű�ͼ�м�ͷ��ʾ��������������0��0������0��1������1��1������1��0��������ÿ������һ����λ����ô��35��ʱ��������λ�õ������ǣ� ��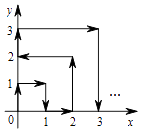
A.��4��0��
B.��5��0��
C.��0��5��
D.��5��5��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com