
����Ŀ���ס���������ĩ��ͬһ�ص����ȥij���㣬������ʱ���£����������ȳ������׳���0.2Сʱ���ҿ�����ǰ���������ʻ��ʱ��Ϊx��h�����ס���������ʻ��·�̷ֱ�Ϊy1��km����y2��km������ͼ����y1��y2����x�ĺ���ͼ�� 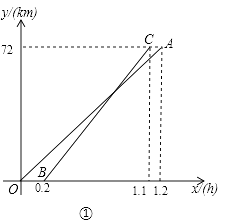
��1���ֱ����߶�OA���߶�BC����ʾ��y1��y2����x�ĺ�������ʽ��
��2����xΪ����ʱ���������6km��
��3�����������Sǧ�ף���ͼ��������ֱ������ϵ�л���S����x�ĺ���ͼ�� 
���𰸡�
��1���⣺��OA��y1=k1x��BC��y2=k2x+b��
��y1=k1x���㣨1.2��72����
����y1=60x��
��y2=k2x+b���㣨0.2��0������1.1��72����
�� ![]() ��
��
��� ![]() ��
��
��y2=80x��16��
��2���⣺��60x=6��
���x=0.1��
��60x����80x��16��=6��
���x=0.5��
��80x��16��60x=6��
���x=1.1��
�ʵ�xΪ0.1��0.5��1.1Сʱ���������6ǧ�ף�
��3���⣺��ͼ��ʾ��
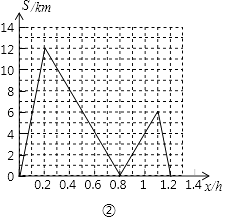
����������1�����ݴ���ϵ���������߶�OA���߶�BC����ʾ��y1��y2����x�ĺ�������ʽ����2����3���������0��x��0.2���ڼס�����������ǰ���ۼס������������������ۿ���x��ֵ����3����4���������0��x��0.2���ڼס�����������ǰ���ۼס��������������ҵ��ᄚ��ǰ���ܼס��������������ҵ��ᄚ��������ۿɻ���S����x�ĺ���ͼ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AD��BC����B��90�㣬EΪAB��һ�㣬�ֱ���ED��ECΪ�ۺ۽������ǣ���A����B���������𣬵�A��Bǡ������CD���ϵĵ�F������AD��2��BC��6����EF��ֵ�ǣ�������
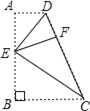
A. 2![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�����ֱ�����ǰ�����ҵ�һԪ���η��̵�ʵ������������ڷ��� ![]() �����������ǣ�
�����������ǣ�
��һ�������ݷ���ϵ��������ȷ��һ�Թ̶���A��0��1����B��5��2��;
�ڶ�����������ƽ�����ƶ�һ��ֱ�����ǰ壬ʹһ��ֱ�DZߺ����A����һ��ֱ�DZߺ����B��
�����������ƶ������У������ǰ��ֱ�Ƕ�������x���ϵ�C��ʱ����C �ĺ�����m��Ϊ�÷��̵�һ��ʵ��������ͼ1��
���IJ����������ǰ�ֱ�Ƕ����λ�ã���������x������һ��D��ʱ����D �ĺ�����Ϊn��Ϊ�÷��̵���һ��ʵ������

��1����ͼ2 �У����ա����IJ����IJ�������������D���뱣��������Dʱֱ�����ǰ�����ֱ�DZߵĺۼ���
��2�����ͼ1����֤�����������������õ���m���Ƿ��� ![]() ��һ��ʵ������
��һ��ʵ������
��3�����������Ĺؼ���ȷ�������̶����λ�ã���Ҫ�Դ˷����ҵ�һԪ���η��� ![]() ��ʵ����������ֱ��д��һ�Թ̶�������ꣻ
��ʵ����������ֱ��д��һ�Թ̶�������ꣻ
��4��ʵ���ϣ���3���еĹ̶����������ԣ�һ���,�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��a��b��c֮�����������Ĺ�ϵʱ����P��
��a��b��c֮�����������Ĺ�ϵʱ����P�� ![]() ��
�� ![]() ����Q��
����Q�� ![]() ��
�� ![]() �����Ƿ���Ҫ���һ�Թ̶��㣿
�����Ƿ���Ҫ���һ�Թ̶��㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=60�㣬OA=OB������C�ӵ�O������������OB�����ƶ�����ACΪ�����Ҳ����ȱ���ACD������BD����BD����ֱ����OA����ֱ�ߵ�λ�ù�ϵ�ǣ�������
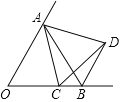
A. ƽ�� B. �ཻ C. ��ֱ D. ƽ�С��ཻ��ֱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C���߶�AB���ӳ����ϣ�AC��![]() BC��D��AB�ķ����ӳ����ϣ�BD��
BC��D��AB�ķ����ӳ����ϣ�BD��![]() DC.
DC.
(1)��ͼ�ϻ�����C�͵�D��λ�ã�
(2)���߶�AB��Ϊx����BC��__ __��AD��__ __��(�ú�x�Ĵ���ʽ��ʾ)
(3)��AB��12 cm�����߶�CD�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��2��ֱ�� �����![]() ��1�����㣬3��ֱ�������
��1�����㣬3��ֱ�������![]() ��3�����㣬4��ֱ�������
��3�����㣬4��ֱ�������![]() ��6�����㣬�����ɴ˲��룬8��ֱ��������ߣߣ�������.
��6�����㣬�����ɴ˲��룬8��ֱ��������ߣߣ�������.

A. 32 B. 16 C. 28 D. 40
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����Ͷ���ӣ��ʵؾ��ȵ������壩��ʵ������Ϸ��
��1����ʵ�������ǹ�����50�����飬���������£�
���ϵĵ��� | 1 | 2 | 3 | 4 | 5 | 6 |
���ֵĴ��� | 10 | 9 | 6 | 9 | 8 | 8 |
����գ��˴�ʵ���У���1�㳯�ϡ���Ƶ���� ��
��2������Ϸʱ����Լ����ÿ��ͬʱ����ö���ӣ������ö���ӵĵ���֮�ͳ���6����С����ʤ������С����ʤ����С����С��˭��ʤ�Ŀ����Դ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����κ���y=ax2+bx��ͼ�����A����1��3��������B�ĺ�����Ϊ1��
��1����������κ����ı���ʽ��
��2����P�ڸö��κ�����ͼ���ϣ���Q��x���ϣ�����A��B��P��QΪ������ı�����ƽ���ı��Σ����P�����ꣻ
��3����ͼ3��һ�κ���y=kx��k��0����ͼ����ö��κ�����ͼ����O��C���㣬��TΪ�ö��κ���ͼ����λ��ֱ��OC�·��Ķ��㣬����T��ֱ��TM��OC������Ϊ��M����M���߶�OC�ϣ�����O��C�غϣ�������T��ֱ��TN��y�ύOC�ڵ�N�����ڵ�T�˶��Ĺ����У� ![]() Ϊ��������ȷ��k��ֵ��
Ϊ��������ȷ��k��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com