2011年3月，英国和新加坡研究人员制造出观测极限为0.000 000 05米的光学显微镜，其中0.000 000 05米用科学记数法表示正确的是（ ）
|
| A． | 0.5×10﹣9米 | B． | 5×10﹣8米 | C． | 5×10﹣9米 | D． | 5×10﹣7米 |
优等生题库系列答案科目：初中数学 来源： 题型：
为了掌握我市中考模拟数学试题的命题质量与难度系数，命题教师赴我市某地选取一个水平相当的初三年级进行调研，命题教师将随机抽取的部分学生成绩（得分为整数，满分为160分）分为5组：第一组85～10；第二组100～115；第三组115～130；第四组130～145；第五组145～160，统计后得到如图所示的频数分布直方图（每组含最小值不含最大值）和扇形统计图，观察图形的信息，回答下列问题：
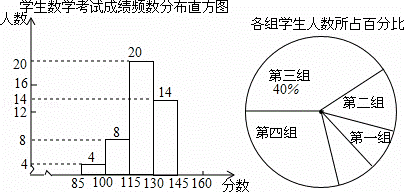
（1）本次调查共随机抽取了该年级多少名学生？并将频数分布直方图补充完整；
（2）若将得分转化为等级，规定：得分低于100分评为“D”，100～130分评为“C”，130～145分评为“B”，145～160分评为“A”，那么该年级1500名考生中，考试成绩评为“B”的学生大约有多少名？
（3）如果第一组只有一名是女生，第五组只有一名是男生，针对考试成绩情况，命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想，请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
填空：
（a﹣b）（a+b）= ；
（a﹣b）（a2+ab+b2）= ；
（a﹣b）（a3+a2b+ab2+b3）= ．
（2）猜想：
（a﹣b）（an﹣1+an﹣2b+…
+abn﹣2+bn﹣1）= （其中n为正整数
，且n≥2）．
（3）利用（2）猜想的结论计算：
29﹣28+27﹣…+23﹣22+2．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，以点O为位似中心，将△ABC放大得到△DEF．若AD=OA，则△ABC与△DEF的面积之比为（ ）
|
| A． | 1：2 | B． | 1：4 | C． | 1：5 | D． | 1：6 |
查看答案和解析>>
科目：初中数学 来源： 题型：
阅读资料：
如图1，在平面之间坐标系xOy中，A，B两点的坐标分别为A（x1，y1），B（x2，y2），由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2，所以A，B两点间的距离为AB= ．
我们知道，圆可以看成到圆心距离等于半径的点的集合，如图2，在平面直角坐标系xoy中，A（x，y）为圆上任意一点，则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2，当⊙O的半径为r时，⊙O的方程可写为：x2+y2=r2．
问题拓展：如果圆心坐标为P（a，b），半径为r，那么⊙P的方程可以写为 （ 综合应用：
如图3，⊙P与x轴相切于原点O，P点坐标为（0，6），A是⊙P上一点，连接OA，使tan∠POA=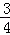
，作PD⊥OA，垂足为D，延长PD交x轴于点B，连接AB．
①证明AB是⊙P的切点；
②是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写出以Q为圆心，以OQ为半径的⊙O的方程；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的整数解的个数是（ ）