把分式方程$\frac{1}{x-2}$-$\frac{1-x}{2-x}$=1化为整式方程正确的是( )A．1-(1-x)=1B．1+(1-x)=1C．1-(1-x)=x-2D．1+(1-x)=x-2 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

11．把分式方程$\frac{1}{x-2}$-$\frac{1-x}{2-x}$=1化为整式方程正确的是（　　）

A．

1-（1-x）=1

B．

1+（1-x）=1

C．

1-（1-x）=x-2

D．

1+（1-x）=x-2

分析分式方程变形后，两边乘以最简公分母（x-2）化简得到结果，即可作出判断．

解答解：方程变形得：$\frac{1}{x-2}$+$\frac{1-x}{x-2}$=1，
去分母得：1+（1-x）=x-2，
故选D

点评此题考查了解分式方程，利用了转化的思想，解分式方程时注意要检验．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

1．

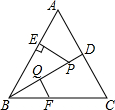如图，△ABC是等边三角形，P是∠ABC的平分线BD上一点，PE⊥AB于点E，线段BP的垂直平分线交BC于点F，垂足为点Q．如果BF=a，那么PE=$\frac{\sqrt{3}}{2}$a（用含a的代数式表示）．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

2．要使分式$\frac{-5}{x-1}$有意义，则x的取值范围是（　　）

A．

x≠1

B．

x＞1

C．

x＜1

D．

x≠-1

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

19．已知m、n是关于x的一元二次方程x²-2x-1=0的两个实数根，则代数式3m²-n²-8m+1的值等于-1．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．

如图，某大街水平地面有两根路灯灯杆AB=CD=10m，小明晚上站在两灯杆的正中位置观察自己眼睛处影子的俯角∠MEG=∠NEH=11.31°，已知地面到小明眼睛处的高度EF=1.5m．
（1）求两灯杆的距离DB；
（2）某县在一条长760m的大街P-K-Q上安装12根灯杆（含两端），其中PK为休闲街，按（1）中的灯杆距离安装灯杆，KQ为购物街，灯杆距离比（1）中的少35m，求休闲街和购物街分别长多少米．
（参考数据：tan78.69°≈5.00，tan11.31°≈0.20，cos78.69°≈0.20，cos11.31°≈0.98，可使用科学计算器）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

16．探究：如图①，在△ABC外作△BAD，△CAE，使∠BAD=∠CAE=90°，AB=AD，AC=AE，以AD，AE为邻边向上作平行四边形ADFE，连接AF，求证：△ADF≌△BAC；
应用：如图②，在图①的基础上，取BD的中点P，连接PF，PC，PA，求∠FPC的度数，并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．计算：
（1）$\sqrt{2}$×$\sqrt{32}$+（$\sqrt{2}$-1）²；
（2）$\frac{x}{{x}^{2}-4}-\frac{1}{2x-4}$；
（3）解方程：$\frac{2x+9}{3x-9}$=$\frac{4x-7}{x-3}$+2；
（4）先化简，再求值：（1-$\frac{1}{a+1}$）÷$\frac{a^2-a}{a+1}$，其中a=$\frac{1}{2}$．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

20．一组数：2，1，3，x，7，-9，…，满足“从第三个数起，前两个数依次为a、b，紧随其后的数就是2a-b”，例如这组数中的第三个数“3”是由“2×2-1”得到的，那么这组数中x表示的数为-1．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

1．已知直角三角形的两条直角边分别为5cm，12cm，则此直角三角形的重心与外心之间的距离是$\frac{13}{6}$cm．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学