
 ,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.
,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.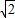 ,写出探索过程.
,写出探索过程.
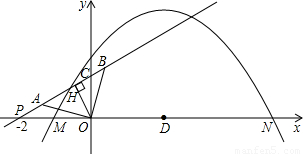 解:(1)∵直线y=kx+b过P(-2,0)?-2k+b=0…①
解:(1)∵直线y=kx+b过P(-2,0)?-2k+b=0…①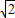 ,AO⊥BO?三角形AOB为等腰直角三角形,
,AO⊥BO?三角形AOB为等腰直角三角形,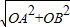 =2?∠OAB=45°?OH=OA×sin45°=1,
=2?∠OAB=45°?OH=OA×sin45°=1,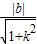 =1…②
=1…②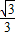 ,b=
,b=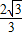 ,OH=1.
,OH=1. .
. (x+1)(x-5).
(x+1)(x-5). x2+
x2+ x+
x+ .
. .
. (x+1)(x-5),
(x+1)(x-5), x2+
x2+ x+
x+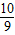 .
. 时,在抛物线y=-
时,在抛物线y=- x2+
x2+ x+
x+ 上存在一点E(2,3)满足条件,
上存在一点E(2,3)满足条件, x2+
x2+ x+
x+ 上,
上, x2+
x2+ x+
x+ 上没有符合条件的其他的E点.
上没有符合条件的其他的E点. 时,同理可得抛物线y=-
时,同理可得抛物线y=- x2+
x2+ x+
x+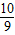 上没有符合条件的其他的E点.
上没有符合条件的其他的E点. x2+
x2+ x+
x+ 时,
时,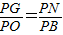 ,
,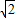 .
. x2+
x2+ x+
x+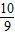 时,
时,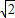 .
.

科目:初中数学 来源:2008年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
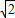 ,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.
,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.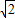 ,写出探索过程.
,写出探索过程.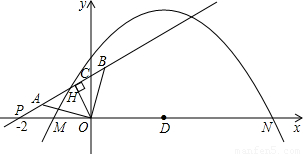
查看答案和解析>>
科目:初中数学 来源:2011年河北省中考数学考前模拟测试精选题(一)(解析版) 题型:解答题
 上运动,湖面风平浪静,双帆远影优美,训练中档教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
上运动,湖面风平浪静,双帆远影优美,训练中档教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).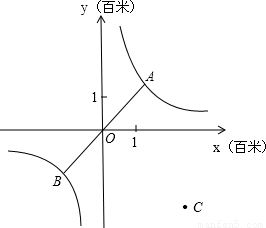
查看答案和解析>>
科目:初中数学 来源:2011年江苏省苏州市中考数学模拟试卷(二)(解析版) 题型:选择题
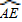 =
= ;④CE×AB=2BD2.其中正确结论的序号是( )
;④CE×AB=2BD2.其中正确结论的序号是( )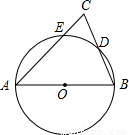
查看答案和解析>>
科目:初中数学 来源:2008年江苏省苏州市中考数学试卷(解析版) 题型:选择题
 =
= ;④CE×AB=2BD2.其中正确结论的序号是( )
;④CE×AB=2BD2.其中正确结论的序号是( )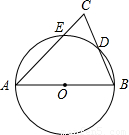
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com