解:(1)
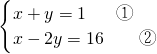
,
由①得:y=1-x ③,
把③代入②得:x-2(1-x)=16,
x-2+2x=16,
3x=18,
x=6,
把x=6代入③得:y=-5,
∴方程组的解为:

,
(2)

,
可变形为:
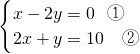
,
由①得:x=2y ③,
把③代入②得:4y+y=10,
y=2,
把y=2代入③得:x=4,
∴方程组的解为:

.
分析:(1)根据观察看出x与y的系数均为1,故用代入法消元较好,把①变形成含x的代数式表示y记作③,再把其代入②便可消去y,解出x的值,再把x的值代入变形后的式子③,即可得到y的值.
(2)首先把方程组化简,再根据观察看出两个式子中均有x与y的系数为1的情况,故用代入法消元较好,把①变形成含y的代数式表示x记作③,再把其代入②便可消去x,解出y的值,再把y的值代入变形后的式子③,即可得到x的值.
点评:此题主要考查了二元一次方程组的解法,解题的关键是消元,消元的方法有两种:①加减法消元,②代入法消元.

 ;
; .
.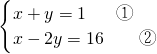 ,
, ,
, ,
,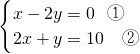 ,
, .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案 (1)解方程组:
(1)解方程组: