
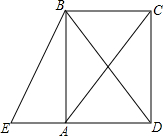
 如图,四边形ABCD是矩形,延长DA至点E,使得AC=BE.
如图,四边形ABCD是矩形,延长DA至点E,使得AC=BE.分析 (1)由矩形的性质得出对角线相等AC=BD,再由已知条件AC=BE,得出BE=BD即可;
(2)由矩形的性质得出∠BAD=90°,AD=BC,AD∥BC,由等腰三角形的三线合一性质得出AE=AD,得出AE=BC,即可得出结论.
解答 证明:(1)∵四边形ABCD是矩形,
∴AC=BD,
∵AC=BE,
∴BE=BD,
即:△BDE是等腰三角形;
(2)∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC,AD∥BC,
∵BE=BD,
∴AE=AD(三线合一),
∴AE=BC,
又∵AE∥BC,
∴四边形AEBC是平行四边形.
点评 本题考查了矩形的性质、等腰三角形的判定与性质、平行四边形的判定;熟练掌握矩形的性质,并能进行推理论证是解决问题的关键.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
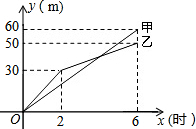 在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
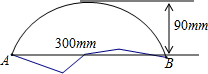 一支考古队发现一个残破的古代圆盘碎片,如图所示,考古家测量了弦AB=300mm,圆弧的高为90mm,于是得到了古圆盘的半径,从而确定了它的圆心,终于使这个古物得以复原,请问你知道考古家怎样得到它的半径吗?
一支考古队发现一个残破的古代圆盘碎片,如图所示,考古家测量了弦AB=300mm,圆弧的高为90mm,于是得到了古圆盘的半径,从而确定了它的圆心,终于使这个古物得以复原,请问你知道考古家怎样得到它的半径吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com